线性回归大结局(岭(Ridge)、 Lasso回归原理、公式推导)，你想要的这里都有

乎语百科 2022-10-01 01:51:06 265 0

本文已参与「新人创作礼」活动，一起开启掘金创作之路。

线性模型简介

所谓线性模型就是通过数据的线性组合来拟合一个数据，比如对于一个数据 $X$

\[X = (x_1, x_2, x_3, ...,x_n) \tag{1} \]

\[Y = f(X) = a_1x_1 + a_2x_2 + ... a_nx_n + b \tag{2} \]

来预测 $Y$的数值。例如对于人的两个属性 (鞋码，体重) 来预测身高。从上面来看线性模型的表达式简单、比较容易建模，但是却有很好的解释性。比如身高$(H)$和鞋码$(S)$、体重$(W)$的关系：

\[H=0.3*S + 0.7*W + 20 \tag{3} \]

所谓解释性简单一点来说就是知道模型哪个属性更加重要，比如说对于上述表达式来说，就意味着对于身高来说体重的因素比较大，体重更加重要，这个例子纯为了解释为什么线性模型有很好的解释性，可能不够严谨。对于线性模型来说，旨在学习到所有的 $a_i, b$，即模型的参数。

普通线性回归

对于一个数据集

\[Dataset = \{ (x_1, y_1), (x_2, y_2), (x_3, y_3), ..., (x_n, y_n) \} \ \ , \ y_i \in R \tag{4} \]

其中 $x_i$, 可能含有多个属性，如 $x_i$ 有$m$个属性时, 即 $x_i = (x_{i1}, x_{i2}, ..., x_{im})$，$y_i$ 是一个实数值。线性回归需要做的事就是需要找到一套参数尽可能的使得模型的输出跟 $y_i$接近。

不妨设如下表达式，我们的目标就是让 $f(x_i)$ 越靠近真实的 $y_i $越好。

\[f(x_i) = a_1x_{i1} + a_2x_{i2} + ... + a_mx_{im} + b \tag{5} \]

即 :

\[f(x_i) = b + \sum_{j = 1}^{m}a_jx_{ij} \tag{6} \]

为了方便使用一个式子表示整个表达式，不妨令 :

\[x_i = (x_{i1}, x_{i2}, ..., x_{im}, 1) \tag{7} \]

\[\hat{w} = (a_1, a_2, ..., a_m, b)^T \tag{8} \]

上述表达式用矩阵形式表示为：

\[\left[ \begin{matrix} x_{i1} & x_{i2} & x_{i3} & ... & x_{i(m - 1)} & x_{im} & 1\end{matrix} \right] \cdot \left[\begin{matrix} a_1 \\ a_2 \\ a_3 \\ .\\.\\. \\ a_{m-1} \\ a_m \\ b\end{matrix} \right] = f(x_i) \tag{9} \]

简写为 :

\[f(x_i) = x_i\cdot \hat{w} \tag{10} \]

现在需要来衡量模型的输出和真实值之间的差异，我们这里使用均方误差$MSE(Mean\ Squared\ Error)$来衡量，即对于 $y_i$来说误差为:

\[\mathcal{l_i} = (f(x_i) - y_i)^2 \tag{11} \]

像这种基于最小化 $MSE$ 来求解模型参数的方法叫做最小二乘法。对于整个数据集来说他的误差为 $\mathcal{L}$ ：

\[\mathcal{L} = \sum_{i = 1}^{n}(f(x_i) - y_i)^2\ \tag{12} \]

现在我们将他们用矩阵来表示其中：

\[Y = (y_1, y_2, y_3, ..., y_{n - 2}, y_{n - 1}, y_{n})^T = \left[\begin{matrix}y_1 \\ y_2 \\ y_3 \\ . \\. \\. \\ y_{n - 2} \\ y_{n - 1}\\ y_{n}\end{matrix}\right] \tag{13} \]

\[X = (x_1; ...; x_n)= (x_1, ..., x_n)^T = \left[\begin{matrix}x_1 \\ x_2 \\ . \\. \\. \\ x_{n-1}\\ x_{n}\end{matrix}\right]= \left[\begin{matrix}x_{11} & x_{12} & x_{13} & . .. & x_{1m} &1& \\ x_{21} & x_{22} & x_{23} & ... & x_{2m} &1& \\ . & . & . & . & . &.\\. & . & . & . & . &. \\ . & . & . & . & . &. \\ x_{(n - 1)1} & x_{(n - 1)2} & x_{(n - 1)3} & ... & x_{(n - 1)m} &1\\ x_{n1} & x_{n2} & x_{n3} & ... & x_{nm} & 1\end{matrix}\right] \tag{14} \]

\[f(X) = \left[\begin{matrix}x_{11} & x_{12} & x_{13} & . .. & x_{1m} &1& \\ x_{21} & x_{22} & x_{23} & ... & x_{2m} &1& \\ . & . & . & . & . &.\\. & . & . & . & . &. \\ . & . & . & . & . &. \\ x_{(n - 1)1} & x_{(n - 1)2} & x_{(n - 1)3} & ... & x_{(n - 1)m} &1\\ x_{n1} & x_{n2} & x_{n3} & ... & x_{nm} & 1\end{matrix}\right] \cdot \left[\begin{matrix} a_1 \\ a_2 \\ a_3 \\ .\\.\\. \\ a_{m-1} \\ a_m \\ b\end{matrix} \right] = \left[\begin{matrix} x_1\hat{w} \\ x_2\hat{w} \\ x_3\hat{w} \\ .\\.\\. \\ x_{n-2}\hat{w} \\ x_{n - 1}\hat{w} \\ x_{n}\hat{w}\end{matrix} \right] = \left[\begin{matrix}\hat{y}_1\\ \hat{y}_2\\ \hat{y}_3\\ \\.\\.\\.\\\hat{y}_{n-2}\\\hat{y}_{n-1}\\\hat{y}_n\\ \end{matrix}\right] \tag{15} \]

其中 $\hat{y}_i$ 是模型的预测值 $y_i$ 是数据的真实值，$m$ 是一条数据 $x_i$的属性的个数。现在来梳理一下数据的维度：

\[X : n\times (m+1) \\ \hat{w} : (m+1)\times 1\\ Y : n\times 1 \\ f(X) : n\times 1 \]

那容易得出，对于整个数据集的误差为 $\mathcal{L}(w, b)$ ：

\[\mathcal{L}(w, b) = \mathcal{L}({\hat{w}}) = \sum_{i=1}^{n}( \hat{y} - y_i)^2 = \sum_{i=1}^{n}(x_i\hat{w}-y_i)^2 = ||X\hat{w}-Y||_2^2 = (X\hat{w}-Y)^T(X\hat{w}-Y) \tag{16} \]

\[x_i = (x_{i1}, x_{i2}, ..., x_{im}, 1)\\ \hat{w} = (a_1, a_2, ..., a_m, b)^T \]

现在来仔细分析一下公式$(16)$，首先对于一个$1\times n$或者$n \times 1$向量来说，它的二范数为：

\[||x||_2 = \sqrt{\sum_{i=1}^{n}x_i^2} \]

二范数平方为：

\[||x||_2^2 = \sum_{i=1}^{n}x_i^2 \]

所以就有了 $\sum_{i=1}^{n}(X\hat{w}-Y)^2 = ||Y-X\hat{w}||_2^2$，那么对于公式$(16)$来说 $X\hat{w}-Y$ 是一个 $n\times 1$的向量：

\[X\hat{w}-Y = \left[\begin{matrix}\hat{y}_1 - y_1 \\ \hat{y}_2 - y_2 \\.\\.\\.\\\hat{y}_{n-1} - y_{n-1} \\\hat{y}_{n}- y_{n} \end{matrix}\right] \]

所以根据矩阵乘法就有：

\[(X\hat{w} - Y)^T(X\hat{w} - Y)=\left[\begin{matrix} \hat{y}_1 - y_1 ,&..., &\hat{y}_{n} - y_{n} \end{matrix}\right]\cdot \left[\begin{matrix}\hat{y}_1 - y_1 \\\hat{y}_2 - y_2 \\.\\.\\.\\\hat{y}_{n-1} - y_{n-1} \\\hat{y}_{n} - y_{n} \end{matrix}\right] = \sum_{i=1}^{n}(\hat{y}- y_i )^2 \tag{17} \]

根据上面的分析最终就得到了模型的误差：

\[\mathcal{L}(w, b) = \mathcal{L(\hat{w})} = ||X\hat{w} - Y||_2^2 = (X\hat{w} - Y)^T(X\hat{w} - Y) \tag{18} \]

现在就需要最小化模型的误差，即优化问题，易知$\mathcal{L(w, b)}$是一个关于 $\hat{w}$ 的凸函数，则当它关于$\hat{w}$导数为0时求出的$\hat{w}$是$\hat{w}$的最优解。这里不对其是凸函数进行解释，如果有时间以后专门写一篇文章来解读。现在就需要对$\hat{w}$进行求导。

\[\mathcal{L(\hat{w})} = ||X\hat{w} - Y||_2^2 = (X\hat{w} - Y)^T(X\hat{w} - Y) \]

\[= ((X\hat{w})^T - Y^T)(X\hat{w} - Y) = (\hat{w}^TX^T - Y^T)(X\hat{w} - Y) \]

\[=\hat{w}^TX^TX\hat{w} - \hat{w}^TX^TY - Y^TX\hat{w} + Y^TY \]

我们现在要对上述公式进行求导，我们先来推导一下矩阵求导法则，请大家扶稳坐好：

公求导式法则一:

$\forall$ 向量 $A:1 \times n$ , $X: n \times 1, Y=A\cdot X$，则 $\frac{\partial Y}{\partial X} = A^T$，其中$Y$是一个实数值。

证明:

不妨设：

\[A = (a_1, a_2, a_3, ..., a_n) \]

\[X = (x_1, x_2, x_3, ..., x_n)^T \]

\[\therefore Y = (a_1, a_2, a_3, ..., a_n)\cdot \left[\begin{matrix} x_1\\x_2\\x_3\\.\\.\\.\\x_n\end{matrix}\right] = \sum_{i = 1}^{n}a_ix_i \]

当我们在对$x_i$，求导的时候其余$x_j, j \neq i$，均可以看做常数，则：

\[\frac{\partial Y}{\partial x_i} = 0 + ...+0 + a_i + 0 +... + 0 \]

\[\therefore \frac{\partial Y}{\partial X} = \left[\begin{matrix}\frac{\partial Y}{\partial x_1}\\ \frac{\partial Y}{\partial x_2}\\.\\.\\.\\ \frac{\partial Y}{\partial x_{n-1}}\\\frac{\partial Y}{\partial x_n}\\\end{matrix}\right] = \left[\begin{matrix}a_1\\ a_2\\.\\.\\.\\a_{n-1}\\ a_n\end{matrix}\right] = (a_1, a_2, a_3, ..., a_n)^T = A^T \]

由上述分析可知：

\[\frac{\partial Y}{\partial X} = A^T \]

公求导式法则二:

当$Y = X^TA$，其中 $X:n\times 1, A:n\times 1$，则$\frac{\partial Y}{\partial X} = A$

公求导式法则三:

当$Y = X^TAX$，其中 $X:1\times n, A : n\times n$，则$\frac{\partial Y}{\partial X} = (A^T + A)X$

上面公式同理可以证明，在这里不进行赘述了。

\[\mathcal{L(\hat{w})} =\hat{w}^TX^TX\hat{w} - \hat{w}^TX^TY - Y^TX\hat{w} + Y^TY \tag{19} \]

有公式$(19)$和上面求导法则可知：

\[\frac{\partial \mathcal{L(\hat{w})}}{\partial \hat{w}} = ((X^TX)^T + X^TX)\hat{w} - X^TY - (Y^TX)^T\\ = 2X^TX\hat{w} - 2X^TY = 2X^T(X\hat{w} - Y) = 0 \]

\[X^TX\hat{w} = X^TY \tag{20} \]

\[\therefore \hat{w}^* = (X^TX)^{-1}X^TY \tag{21} \]

即 $\hat{w}^* = (X^TX)^{-1}X^TY$ 为我们要求的参数。

Ridge(岭)回归

写在前面：对于一个矩阵 $A_{n\times n}$ 来说如果想它的逆矩阵那么 $A$ 的行列式必然不为0，且矩阵 $A$ 是一个满秩矩阵，即$r(A)=n$。

根据上面的推导，在由公式$(20)$ 到 $(21)$ 是等式两遍同时乘了 $X^TX$ 的逆矩阵，但是实际情况中，矩阵的逆可能是不存在的，当矩阵 $X^TX : n\times n$ 不是满秩矩阵的时候，即 $r(X^TX) < n$即 $X^TX$ 行列式为 0时， $(X^TX)^{-1}$ 不存在。一种常见的情况是，当 $x$ 的的样本数据小于他的维数的时候，即对于 $X$ 来说 $n<m$，那么$r(X) < m$ ，又根据矩阵性质 $r(X) = r(X^T) = r(X^TX)$，可以得到 $r(X^TX) < m$，那么 $X^TX$ 不满秩，则 $(X^TX)^{-1}$ 不存在。

对于上述 $(X^TX)^{-1}$ 不存在的情况一种常见的解决办法就是在损失函数 $\mathcal{L(\hat{w})}$ 后面加一个$L_2$正则化惩罚项：

\[\mathcal{L(\hat{w})} = ||X\hat{w} - Y||_2^2 + \lambda||\hat{w}||_2^2 = (X\hat{w} - Y)^T(X\hat{w} - Y) + \lambda\hat{w}^T\hat{w} \tag{22} \]

则对 $\hat{w}$ 求导有：

\[\frac{\partial \mathcal{L(\hat{w})}}{\partial \hat{w}} = 2X^TX\hat{w} - 2X^TY + 2\lambda\hat{w} = 0 \tag{23} \]

\[(X^TX+\lambda E)\hat{w} = X^TY \]

当 $X^TX$ 不满秩的时候，其行列式为0，加上 $\lambda E$之后可以使得 $X^TX+\lambda E$ 行列是不为0，所以 $(X^TX+\lambda E)^{-1}$存在则：

\[\hat{w} = (X^TX+\lambda E)^{-1}X^TY \tag{24} \]

除了上面提到的$X^TX$不满秩的情况，还有一种常见的就是数据之间的共线性的问题，它也会导致$X^TX$的行列式为0，即$X^TX$不满秩。简单来说就是数据的其中的一个属性和另外一个属性有某种线性关系，也就是说这两个属性就相当于一个属性，因为其中一个属性可以用另外一个属性线性表示。这会让模型再训练的时候导致过拟合，因为模型再训练的时候不会去关心属性之间是否具有线性关系，模型只会不加思考的去降低整个模型的损失，即$MSE$，这会让模型捕捉不到数据之间的关系，而只是单纯的去降低训练集的$MSE$。而你如果只是单纯的去降低你训练集的$MSE$的时候，没有捕捉到数据的规律，那么模型再测试集上会出现比较差的情况，即模型会出现过拟合的现象。

为什么正则化惩罚项Work?

上面谈到模型出现过拟合的现象，而加上$L_2$损失可以一直过拟合现象，我在这里简单给大家说说我得观点，不一定正确，希望可以帮助大家理解为什么$L_2$惩罚项可以在一定程度上抑制过拟合现象。首先看一下真实数据：

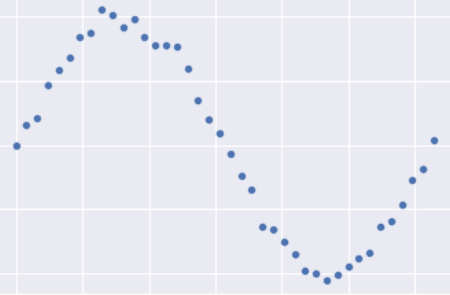
如果需要拟合的话，下面的结果应该是最好的，即一个正弦函数：

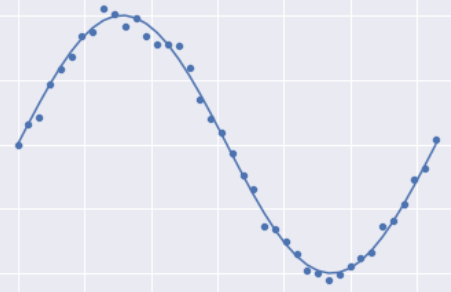
下图是一个过拟合的情况：

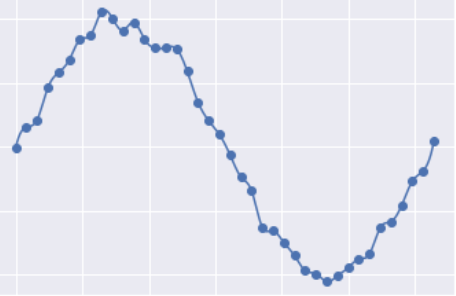
我们可以观察一下它真实规律正弦曲线的之间的差异：过拟合的曲线将每个点都考虑到了，因此他会有一个非常大的缺点就是”突变“，即曲线的斜率的绝对值非常大，如：

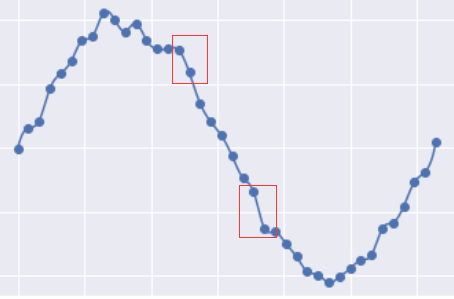
对于一般的一次函数 $y = ax + b$ 来说，当 $a$ 很大的时候，斜率会很大，推广到复杂模型也是一样的，当模型参数很大的时候模型可能会发生剧烈的变化，即可能发生过拟合现象。现在我们来看为什么在线性回归中加入了一个 $L_2$ 惩罚项会减少过拟合的现象。因为在损失函数中有权重的二范数的平方，当权重过大的时候模型的损失就会越大，但是模型需要降低损失，那么就需要降低权重的值，权重的值一旦低下来，突变的可能性就会变小，因此在一定程度上可以抑制过拟合现象。而参数 $\alpha$ 就是来调控权重在损失中的比例，当 $\lambda$ 越大的时候对权重惩罚的越狠，这在实际调参的过程中需要了解。后面的 $Lasso$ 回归参数 $\alpha$ 的意义也是相似的。

Lasso回归

岭回归是在损失函数中加一个$L_2$损失，而$Lasso$回归是在损失函数$\mathcal{L(\hat{w})}$后面加一个$L_1$的损失，即：

\[\mathcal{L(\hat{w})} = ||X\hat{w} - Y||_2^2 + \alpha\sum_{j=0}^{m}|{\hat{w}}_j| \tag{25} \]

对公式$(25)$求导：

\[\frac{\partial \mathcal{L(\hat{w})}}{\partial \hat{w}} = 2X^TX\hat{w} - 2X^TY + \alpha C = 0 \tag{26}\\ \]

\[\left\{\begin{matrix}c_i = -1\ ,\ if\ \hat{w}_i < 0;\\ c_i = 1\ ,\ if\ \hat{w}_i \ge 0;\\\end{matrix}\right. \]

其中$C$是和$\hat{w}$同维度的向量。则可以得到：

\[\hat{w} = (X^TX)^{-1}(X^TY-\frac{\alpha}{2} C)\tag{27} \]

线性回归实现过程

上面提到$\mathcal{L(w, b)}$是一个关于 $\hat{w}$ 的凸函数，则当它关于$\hat{w}$导数为0时求出的$\hat{w}$是$\hat{w}$的最优解，因此在编码实现线性回归的过程中，如果数据集比较小可以直接将所有的数据同时进行计算，节省计算资源，因为只需要计算一次 $\hat{w}$ 的导数。但是如果数据量过大的话，计算无法一次性完成，可以使用随机梯度下降法，或者其他的优化算法，进行多次迭代学习，得到最终的结果。

Ridge回归和Lasso回归区别

上面谈到了 $Ridge$ 和 $Lasso$ 的具体的实现方法，还简要谈到了 $Ridge$ 可以有效防止模型过拟合，和他在数据个数小于数据维度的时候的使用。那么都是增加一个惩罚项，那么 $Ridge$ 和 $Lasso$ 有什么区别呢？

$Ridge$ 和 $Lasso$ 都可以在一定程度上防止模型过拟合
$Ridge$ 在数据个数小于数据维度的时候比较适合
$Lasso$ 的数据的属性之间有共线性的时候比较适合
$Ridge$ 会限制参数的大小，使他逼近于0
$Lasso$ 是一种稀疏模型，可以做特征选择

为什么 $Lasso$ 是一种稀疏模型，因为它在训练的过程中可以使得权重 $\hat{w}$ 中的某些值变成0（稀疏权重），如果一个属性对应的权重为0，那么该属性在最终的预测当中并没有发挥作用，这就相当与模型选择了部分属性(他们你的权重不为0)。我们很容易知道既然这些属性对应的权值为0，即他对于模型来说并不重要，模型只选择了些权重不为0的属性，所以说 $Lasso$ 可以做特征选择。而$Ridge$ 也会不断降低权值的大小，但是他不会让权值变成0，只会不断的缩小权值，使其逼近于0。

Ridge和Lasso对权值的影响

在正式讨论这个问题之间我们首先先来分析不同的权值所对应的$RSS$（残差平方和）值是多少。$RSS$的定义如下：

\[RSS = \sum_{i=0}^{n}(x_i\hat{w} - y_i)^2 \]

对于一个只有两个属性的数据，对不同的权值计算整个数据集在相应权值下的 $RSS$ 。然后将 $RSS$ 值相等的点连接起来做成一个等高线图，看看相同的$RSS$ 值下权值围成了一个什么图形。

对于一个只有两个属性的数据，他的参数为 $\hat{w} = (\hat{w_1}, \hat{w_2})$，然后计算在参数$\hat{w}$ 的情况下，计算整个数据集的 $RSS$ ：数据点的坐标就是 $(\hat{w}_1, \hat{w}_2)$，等高线的高度就是 $RSS$。

比如我们有两个属性 $x_1, x_2$ 它们有一个线性组合 $y = 0.2 * x1 + 0.1 * x2$ 很容易直到 $y$ 和 $x_1, x_2$ 之间是一个线性组合关系：

\[y = \left[\begin{matrix} x_1, x_2\end{matrix}\right] \cdot \left[\begin{matrix} 0.2 \\ 0.1\end{matrix}\right] \]

即我们要求的权值 $\hat{w} = \left[\begin{matrix} 0.2 \\ 0.1\end{matrix}\right]$ 因为和真实值一样，所以它对应的 $RSS$ 为0。我们现在要做的就是针对不同的 $\hat{w}$ 的取值去计算其所对应的 $RSS$ 值。比如说 $\hat{w}$ 取到下面图中的所有的点。然后去计算这些点对应的 $RSS$ ，然后将 $RSS$ 值作为等高线图中点对应的高，再将 $RSS$ 相同的点连接起来就构成了等高线图。

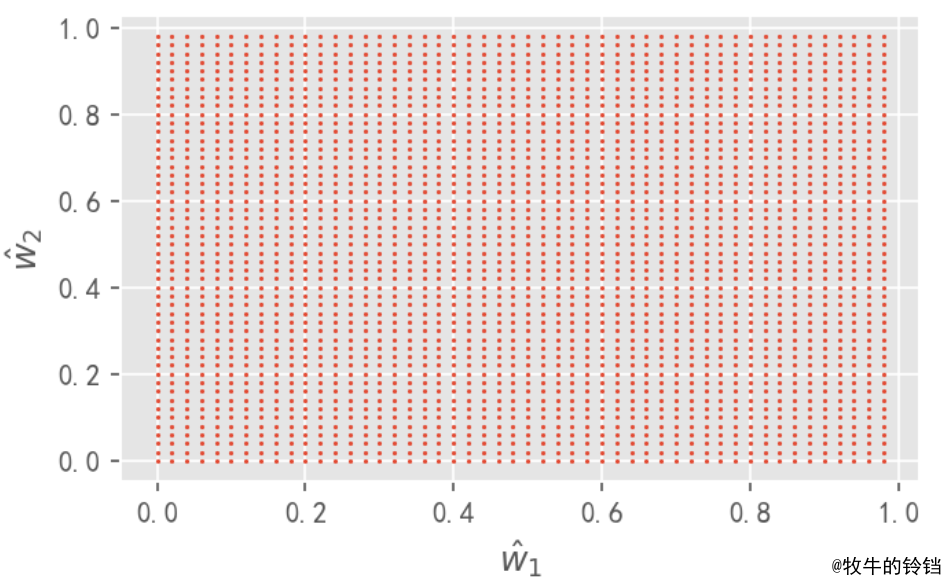
下面就是具体的生成过程：

首先先生成一个随机数据集

import numpy as np
from matplotlib import pyplot as plt
import matplotlib as mpl
plt.style.use("ggplot")

x1 = np.linspace(0, 20, 20)
x2 = np.linspace(-10, 10, 20)
y = .2 * x1 + .1 * x2
# y 是 x1 和 x2的线性组合 所以我们最终线性回归要求的参数为 [0.2, 0.1]

x1:
array([ 0.        ,  1.05263158,  2.10526316,  3.15789474,  4.21052632,
        5.26315789,  6.31578947,  7.36842105,  8.42105263,  9.47368421,
       10.52631579, 11.57894737, 12.63157895, 13.68421053, 14.73684211,
       15.78947368, 16.84210526, 17.89473684, 18.94736842, 20.        ])
x2:
array([-10.        ,  -8.94736842,  -7.89473684,  -6.84210526,
        -5.78947368,  -4.73684211,  -3.68421053,  -2.63157895,
        -1.57894737,  -0.52631579,   0.52631579,   1.57894737,
         2.63157895,   3.68421053,   4.73684211,   5.78947368,
         6.84210526,   7.89473684,   8.94736842,  10.        ])

# 先将 x1 x2 进行拼接
data = np.vstack((x1, x2)).T

data:
array([[  0.        , -10.        ],
       [  1.05263158,  -8.94736842],
       [  2.10526316,  -7.89473684],
       [  3.15789474,  -6.84210526],
       [  4.21052632,  -5.78947368],
       [  5.26315789,  -4.73684211],
       [  6.31578947,  -3.68421053],
       [  7.36842105,  -2.63157895],
       [  8.42105263,  -1.57894737],
       [  9.47368421,  -0.52631579],
       [ 10.52631579,   0.52631579],
       [ 11.57894737,   1.57894737],
       [ 12.63157895,   2.63157895],
       [ 13.68421053,   3.68421053],
       [ 14.73684211,   4.73684211],
       [ 15.78947368,   5.78947368],
       [ 16.84210526,   6.84210526],
       [ 17.89473684,   7.89473684],
       [ 18.94736842,   8.94736842],
       [ 20.        ,  10.        ]])

x_max = 0.5
points = 5000
xx, yy = np.meshgrid(np.linspace(-x_max, x_max, points), np.linspace(-x_max, x_max, points))
zz = np.zeros_like(xx)
for i in range(points):
    for j in range(points):
        beta = np.array([xx[i][j], yy[i][j]]).T
        rss = ((data@beta - y) ** 2).sum()
        zz[i][j] = rss
plt.contour(xx, yy, zz, levels=30, cmap=plt.cm.Accent, linewidths=1)
sns.scatterplot(x=[0, 0.2], y=[0, 0.1], s=10)
plt.text(x=0.2, y=0.1, s=r"$\hat{w}(0.2, 0.1)$", fontdict={"size":8})
plt.text(x=0, y=0, s=r"$O(0, 0)$", fontdict={"size":8})
plt.xlim(-.2,.5)
plt.xlabel(r"$\hat{w}_1$")
plt.ylabel(r"$\hat{w}_2$")
plt.show()

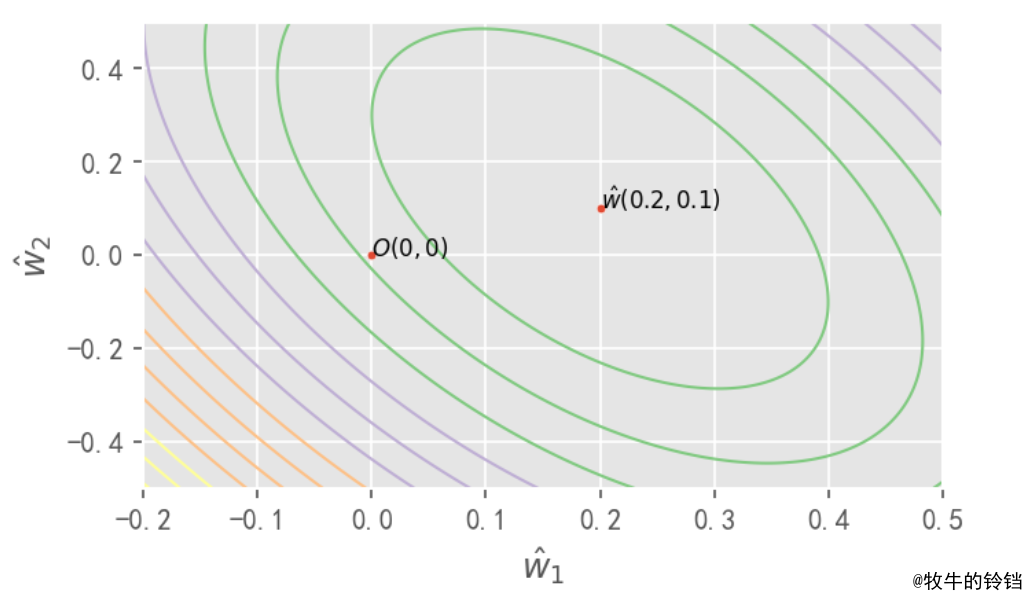
我们最终需要求的 $\hat{w}$ 是 $(0.2, 0.1)$ 同时我们也计算了其他位置对应整个数据集的 $RSS$。我么容易看出等高线都是以 $\hat{w}(0.2, 0.1)$ 为圆心的椭圆，如果需要证明需要使用数学进行严格推到，这里我们只需要直到它的轨迹是一个椭圆即可，而我们知道

\[{\hat{w}_1^2} +{\hat{w}_1^2}\le C \]

$||\hat{w}||_2^2$ 的取值范围是一个圆，因为在岭回归损失函数的式子中有着两部分，它要同时满足这两个条件，那么他们两个曲线的交点就是 $Ridge$ 的权重的取值，如下图所示：

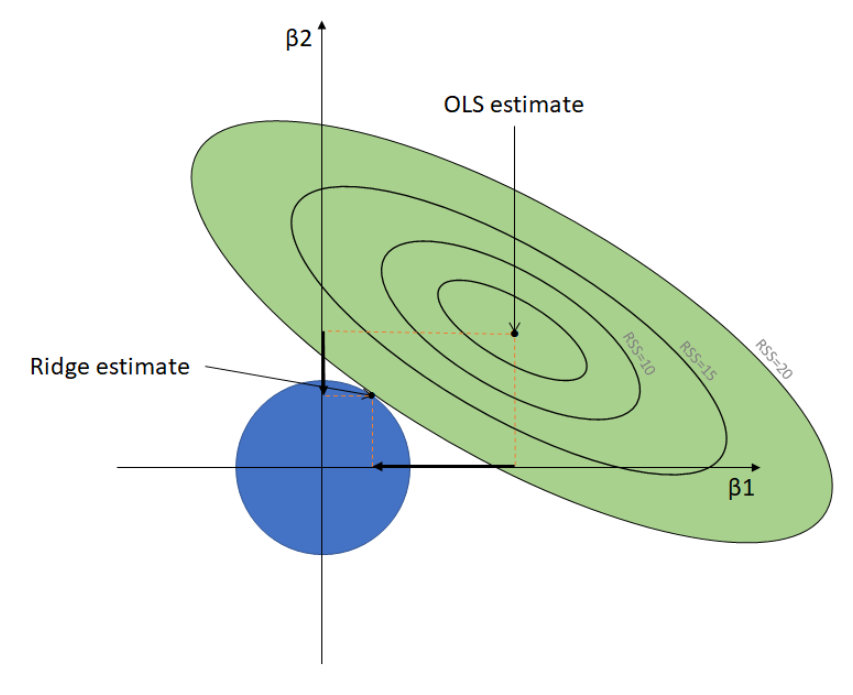
我们从上面的图很容易看出，最终两个权值的取值不会为0（如果为0他们的交点会在x或者y轴上），而是会随着权值的缩小而不断变小，即图中蓝色部分变小。同理我们也可以对 $Lasso$ 回归最同样的事儿：

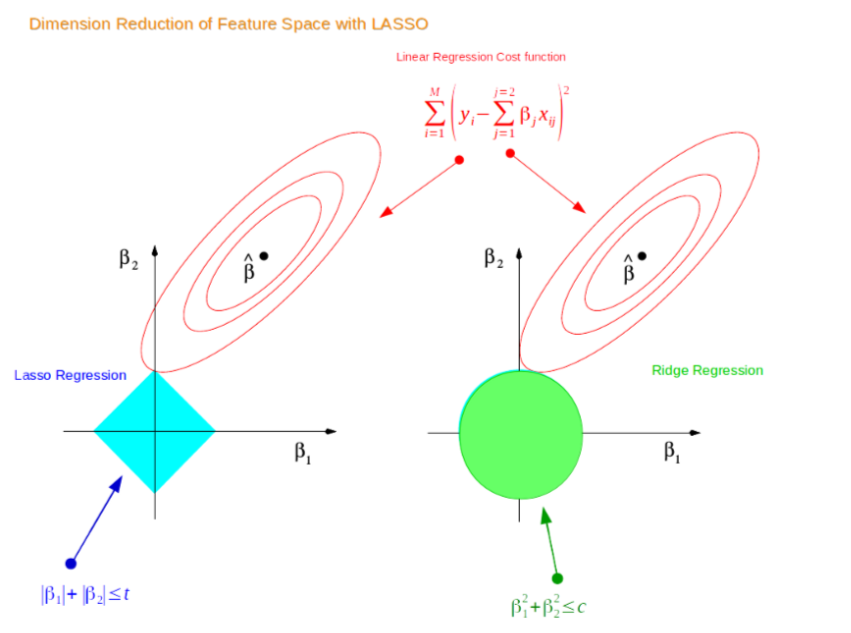
从上图可以看出 $Lasso$ 的权值是可以取到0的，注意是可以取到而不是一定取到，可以取到就说明，$Lasso$ 回归可以在数据集有共线性的时候，对属性进行选择，即让某些属性对应的权值为0。上面的结论都是在二维情况下产生的，可以推广到高维数据。以上就说明了在线性回归中 $Ridge$ 和 $Lasso$ 对权值的影响。

以上就是本篇文章的所有内容了，我是LeHung，我们下期再见！！！更多精彩内容合集可访问项目：https://github.com/Chang-LeHung/CSCore

关注公众号：一无是处的研究僧，了解更多计算机（Java、Python、计算机系统基础、算法与数据结构）知识。

标签：