论文信息
论文标题:Towards Robust False Information Detection on Social Networks with Contrastive Learning论文作者:Chunyuan Yuan, Qianwen Ma, Wei Zhou, Jizhong Han, Songlin Hu论文来源:2019,CIKM论文地址:download 论文代码:download
1 Introduction
问题:会话图中轻微的扰动讲导致现有模型的预测崩溃。
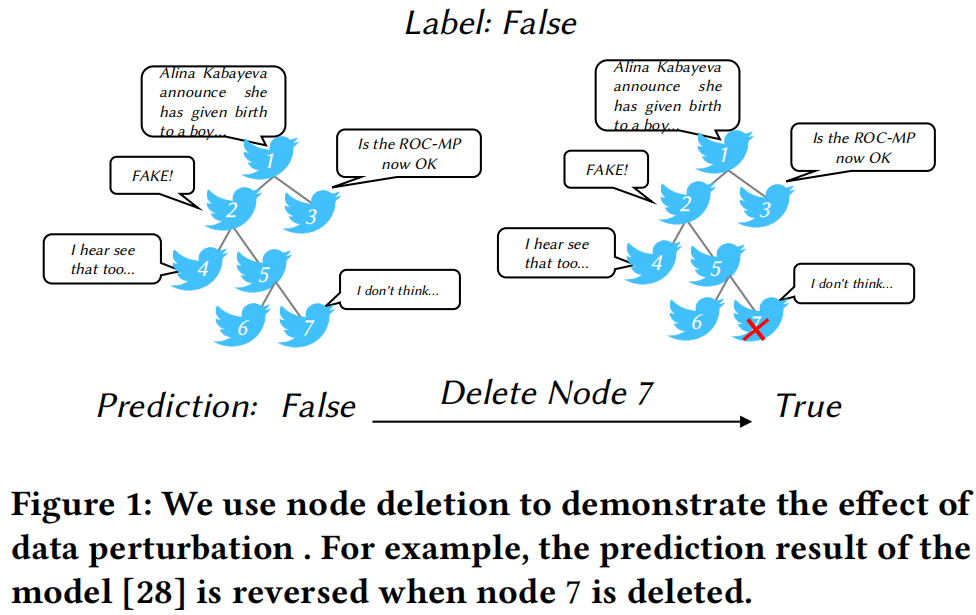
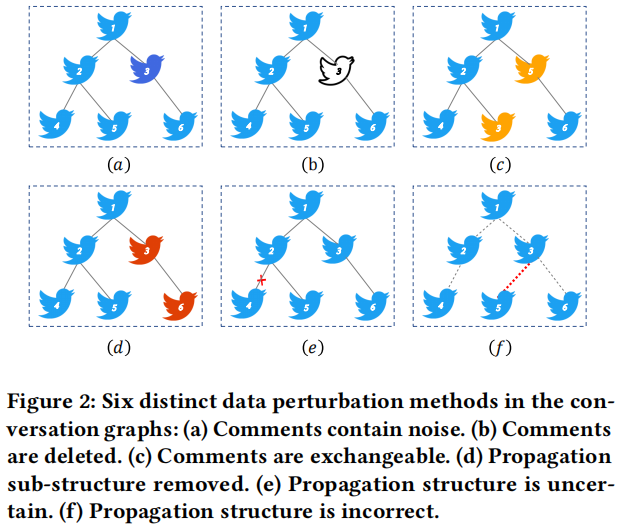
研究了两大类数据增强策略(破坏会话图结构):
贡献:
(1) 提出了RDCL框架,为虚假信息检测提供了鲁棒的检测结果,该框架利用对比学习从多个角度提高了模型对扰动信号的感知。
(2) 证明了硬正样本对可以提高对比学习的效果。
(3) 提出了一种有效的硬样本对生成方法 HPG,它可以增加对比学习的效果,使模型学习更鲁棒的表示。
(4) 通过比较实验、在不同的 GNN 和两个数据集上进行的消融实验,证明了该模型的有效性。
2 Methodlogy
问题定义:预测无向会话图的标签。
整体框架如下:

2.1 Data Perturbations
在除根节点以外的节点中,以 $\rho $ 的采样率采样节点,对于采样的节点用高斯分布初始化,没有被采样到的节点采用 0 填充:
$X_{C N}^{-r}=X^{-r}+X_{G a u s s i o n}^{-r}$
Comments are deleted (CD)
在除根节点以外的节点中,以 $\rho $ 的采样率采样节点,然后将其节点特征向量置 0 :
$X_{C D}^{-r}=X^{-r} \odot D^{-r}$
Comments are exchangeable (CE)
在除根节点以外的节点中,以 $\rho $ 的采样率采样节点,交换节点特征向量。
Propagation sub-structure is removed (PR)
在除根节点以外的节点中,随机选择一部分节点,并删除其形成的子图。
以 $\rho $ 的采样率采样边,并删除边:
$A_{P U}=A-A_{\text {drop }}$
随机选择两个节点 $C_i$ 和 $C_j$,对于 节点 $C_i$,选择删除它和它父节点之间的边,并添加 $C_j$ 和 $C_i$ 之间的边。
2.2 Contrastive Perturbation Learning
假设:对于含有相同标签的图,将他们认为是正样本对,每个 batch 中有 $P$ 张图,加上数据增强后生成的 $2P$ 张图,总共有 $3P$ 张图,自监督对比损失如下:
${\large \mathcal{L}_{S C L}=-\frac{1}{3 P} \log \frac{\sum\limits _{Y_{s}=Y_{m}} \exp \left(z_{m} \cdot z_{s} / \tau\right)}{\sum\limits_{Y_{s}=Y_{m}} \exp \left(z_{m} \cdot z_{s} / \tau\right)+\sum\limits_{Y_{d} \neq Y_{m}} \exp \left(z_{m} \cdot z_{d} / \tau\right)}} $
[ Anchor 和 数据增强图之间的对比损失]
2.3 Perturbation Sample Pairs Generation
自监督损失:
$\begin{aligned}\mathcal{L}_{\mathrm{SSL}}=&-z_{m}^{i} \cdot z_{m}^{j} / \tau +\log \left(\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{\mathrm{Neg}} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)\right)\end{aligned}$
[数据增强图之间的对比损失]
上述 $\mathcal{L}_{\text {SSL }}$ 关于 $z_{m}^{i}$ 的梯度为:
$\begin{aligned}\frac{\partial \mathcal{L}_{S S L}}{\partial z_{m}^{i}} &=-\frac{1}{\tau}\left(z_{m}^{j}-\frac{\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right) z_{m}^{j}+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right) z_{n e g}}{\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)}\right) \\&=-\frac{\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)\left(z_{m}^{j}-z_{m}^{i}\right)-\left(z_{n e g}-z_{m}^{i}\right)}{\tau \exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g}\right) / \tau} \\&=-\frac{1}{C_{1} \tau}\left(\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)\left(z_{m}^{j}-z_{m}^{i}\right)+C_{2}\right)\end{aligned}$
其中:
$C_{1}=\exp \left(z_{m}^{i} \cdot z_{m}^{j} / \tau\right)+\sum\limits_{N e g} \exp \left(z_{m}^{i} \cdot z_{n e g} / \tau\right)$
$C_{2}=z_{n e g}-z_{m}^{i}$
$\text{Eq.7}$ 在分子中的梯度贡献主要来自于($z_{m}^{j}-z_{m}^{i}$)。因此,如果能够增加图级空间中样本对之间的距离,它将提供更大的梯度信号,从而增加模型的学习难度,提高对比学习的质量。所以,本文的对比视图生成方法如下:
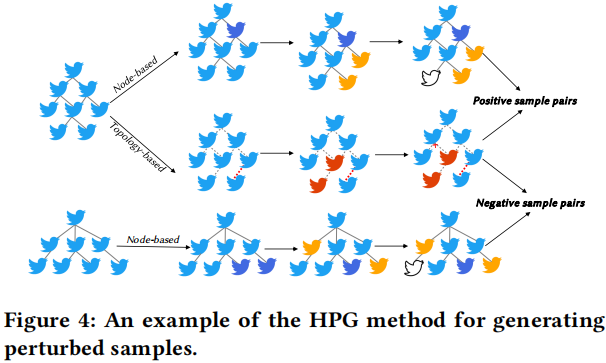
Figure 5 说明,由 HPG 生成的数据增强图,他们之间的相似度小于其他数据增强方法,那么损失函数 SSL 会加大对模型的惩罚,提高对比学习的质量。

虽然扰动会加大学习的难度,但是他们提供了足够的信息去保存视图之间的一致性。
2.4 Training Objective
3 Experiment
3.1 Datasets
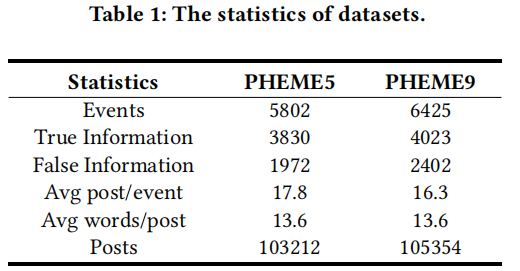
3.2 Performance Comparison

3.3 Robustness Studies
基于本文的 6 中数据增强策略,对比 GACL 和本文方法:
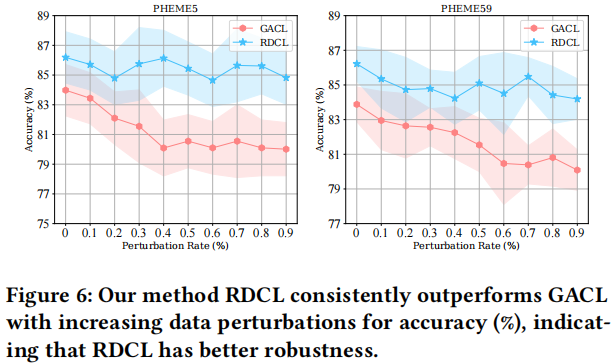
3.4 The robustness on different perturbation scenarios
研究采用复杂数据增强策略组合的对比实验:
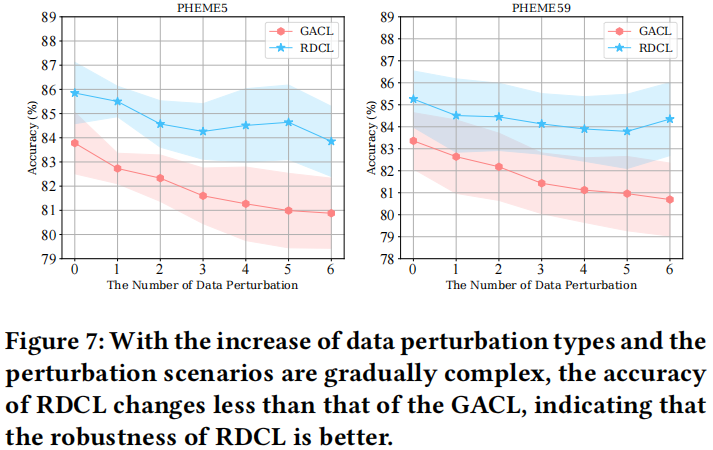
3.5 Ablation Studies
研究如下 6 中数据增强策略 Node Mask , Edge Drop , Mixed , Node-based, Topology-based and our method HPG 的实验对比结果:
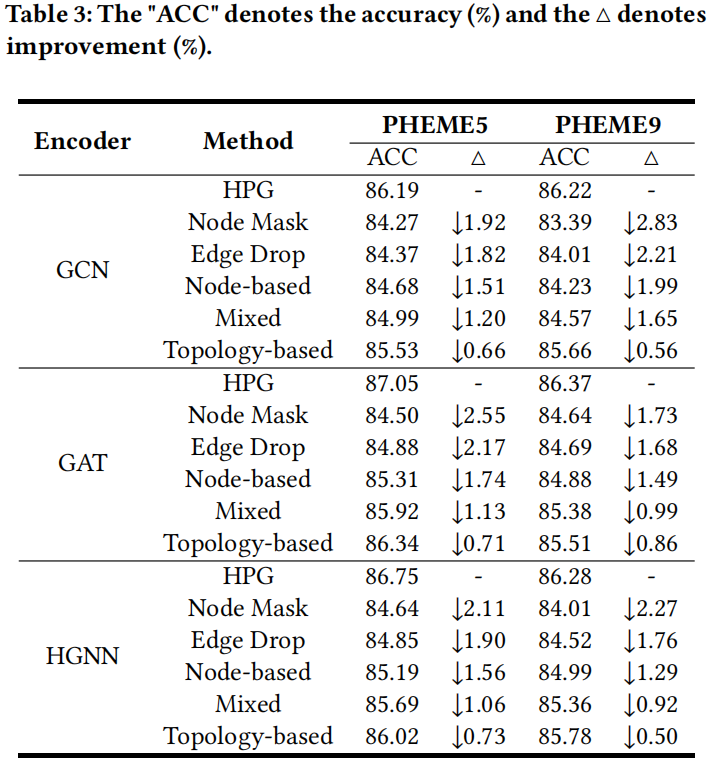
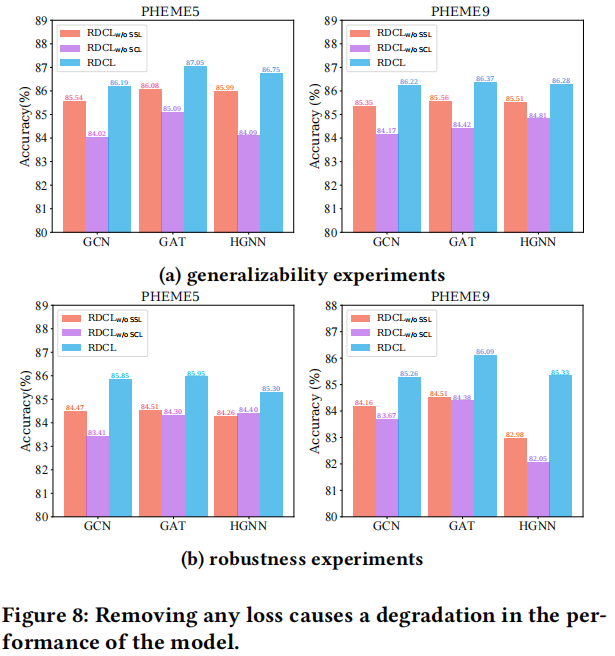
3.6 Graph-level Representation Studies
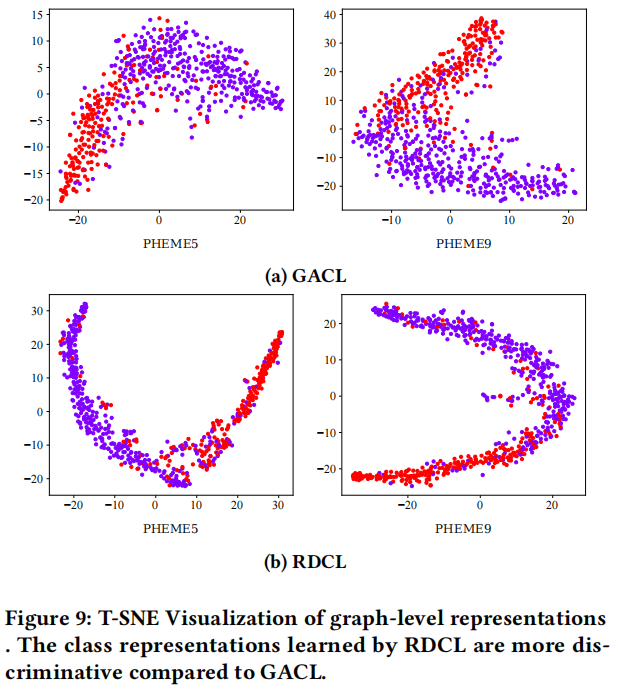
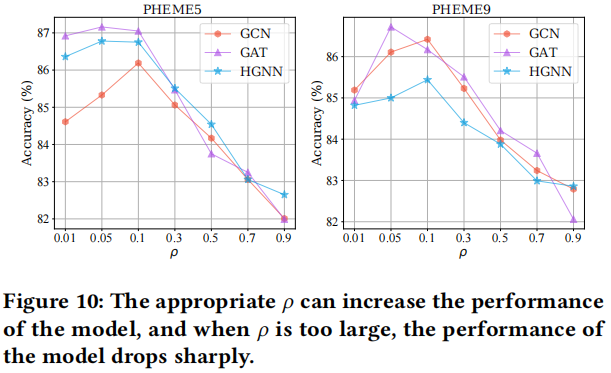
3.7 The Impact of Perturbation Probability $\rho$
不同扰动率 和 不同编码器的实验对比:
标签:

留言评论