前言
[失踪人口回归 (*/ω\*)] 真的好久好久没有更新了,因为自己也还在找方向,但还是把新学的知识记录在博客里。今天要介绍的是BLS签名算法。
一、BLS签名算法简介
BLS签名算法[1]是由斯坦福大学的 Dan Boneh、Ben Lynn 和 Hovav Shacham一同提出的。
一般将 ECDSA签名算法、Schnorr签名算法和BLS进行对比。
ECDSA签名算法局限性:
无法进行签名聚合和密钥聚合。换句话说,当我们验证多重签名交易的时候,我们只能逐个对签名进行验证,显然这会耗费大量的区块空间和交易费。因此并不适用于多重签名场景。
Schnorr签名算法:
可以将一笔交易中的所有签名和公钥合并成单个签名和公钥,其过程是不可见的(即无法判断该签名或公钥是否通过合并得到的)。这样就可以实现只需要一次就可以对合并后的签名做验证,加快了区块验证的速度。
但其仍然存在着局限性:
多重签名需要多次(签名者之间的)通信,这对冷钱包来说过于麻烦;
聚合签名算法依赖随机数生成器,而不像 ECDSA 那样可以使用指定的随机点(R);
m-n 多重签名机制比较取巧,需要构建公钥的默克尔树。当 m 和 n 较大时,树所占空间会相当大;
无法把一个区块中的所有签名聚合成一个签名。
与这两个签名算法作比较,BLS有如下优点:
(1)不需要随机数生成器,可以将区块中的所有签名聚合成一个;
(2)容易实现 m-n 多重签名,也可以避免签名者之间的多余通信;
(3)签名的长度更短(签名为椭圆曲线上的一个点而非两个),是 Schnorr 或 ECDSA 的 2 分之一。
二、基础知识
在对BLS算法进行阐述之前,首先了解一下曲线哈希和曲线配对。
2.1 曲线哈希
Hashing to the curve 一般可以翻译为曲线哈希或者是哈希成曲线上的点。没了解之前听到曲线哈希可能会不知道是啥,但听到哈希成曲线上的点就大概知道意思了。
在一般的哈希计算中,常常是对于不定长的输入最终输出一个定长的数值。但曲线哈希就不一样,其输出结果会对应到椭圆曲线上的一个点。
具体做法如下:
哈希函数保持不变,将得到的哈希值作为点的 x 值寻找椭圆曲线上的对应点。
通常来说(比如比特币所用的曲线),椭圆曲线有 2256 个点,而 SHA-256 哈希算法的值是 256 位。不过,一个有效的 x 坐标,会对应一正一负两个 y 坐标(因为(x, y)和(x, -y)都是曲线y²=x³+ax+b上的点)。换句话说,新的哈希算法大约有 50% 的概率在曲线上找到 2 个对应点,另 50% 的概率则一个点也找不到。因此,在应用过程中会出现需要尝试多次才能找到对应点的情况。
· 有两个对应点怎么解决呢?
选择y坐标较小的作为结果即可。
· 那出现找不到对应点的情况怎么办呢?
可以在消息体后面附加一个数。当找不到对应点的时候,将该数加一再重新计算直到找到对应的点。
下面给出一个例子。
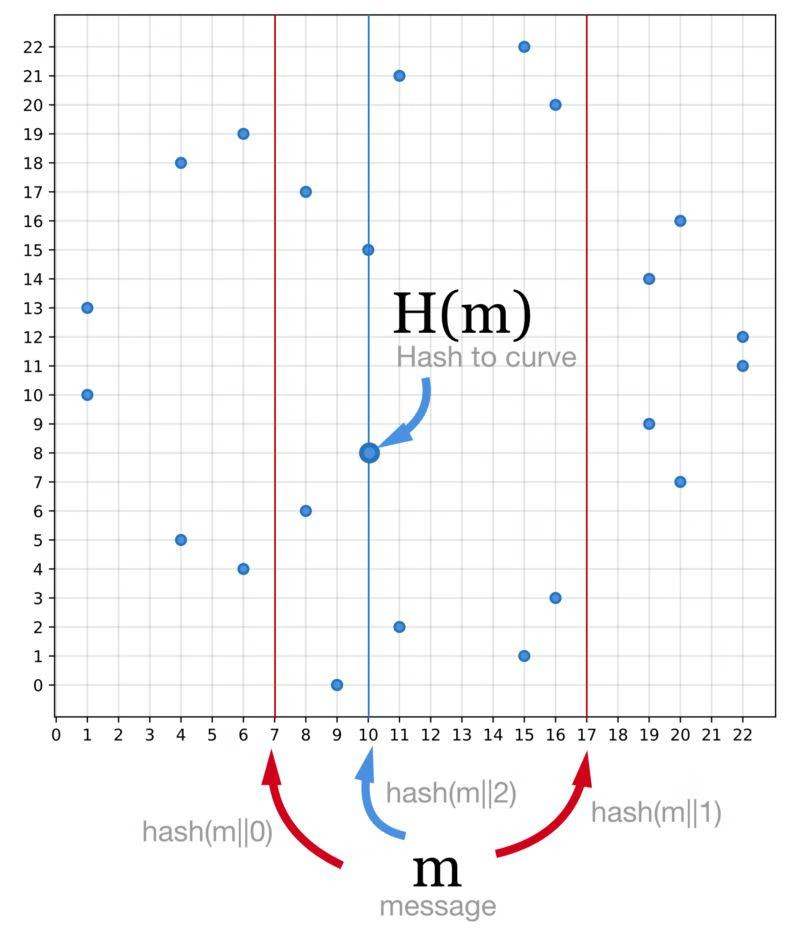
以在模为 23 的有限域上定义的椭圆曲线 y²=x³+7为例。只有一半的 x 坐标在曲线上能找到对应点。
① 计算 hash(m||0),没有对应的点。
② 计算 hash(m||1),没有对应的点。
③ 计算 hash(m||2),发现对应的点。对应的点有两个,选择y坐标较小的作为结果。
2.2 曲线配对
在曲线哈希中,我们将输入(一个值)映射到一个椭圆曲线上的点。显然,我们还需要能将点映射为数的函数。下面介绍一种特殊的函数,这种函数能够把一条(或 2 条不同的)曲线上的两个点 P 和 Q映射为一个数:
e ( P , Q ) → n
此函数还要有一个重要的特性。即对于未知数 x 和两个点 P 、 Q ,无论哪个点乘以 x,结果相同,即:
e ( xP , Q ) = e ( P , xQ )
该函数还有如下性质:
e ( aP , bQ ) = e ( P , abQ ) = e ( abP , Q ) = e ( bP , aQ ) = e ( P , Q ) ab
这里就不对该函数的原理进行详细介绍,里面涉及到许多数学原理。但不出意外的话,我后面会更新一篇关于配对(pairings)的理论,感兴趣的话可以关注一下。
现在就只需要知道这种函数是存在的,并且它们有上面介绍的性质。除此之外,它并不会暴露x的任何信息。
值得注意的是,配对函数中不能使用任何椭圆曲线(特别是比特币的 secp256k1 椭圆曲线)。我们必须使用非常特殊的曲线(通常出自易于配对的曲线簇),才能保证函数的效率和安全。
三、BLS签名方案
现在终于能进入正题啦!
下面用 pk 表示私钥, P 表示公钥, m 表示待签名的消息。其中 P = pk×G.
3.1 签名
① 对消息m 进行曲线哈希得到H(m).
② 使用私钥进行签名。将刚刚得到的结果乘以私钥。
S = pk × H(m)
3.2 验证签名
在验证签名的时候,使用公钥 P 进行验证。验证过程如下:
e ( P , H(m) ) = e ( G , S )
3.3 原理
下面证明 e ( P , H(m) ) = e ( G , S ) 该等式成立。
已知:P = pk×G ,e ( xP , Q ) = e ( P , xQ ) .
e ( P , H(m) ) = e ( pk × G, H(m) ) = e ( G , pk × H(m) ) = e ( G , S )
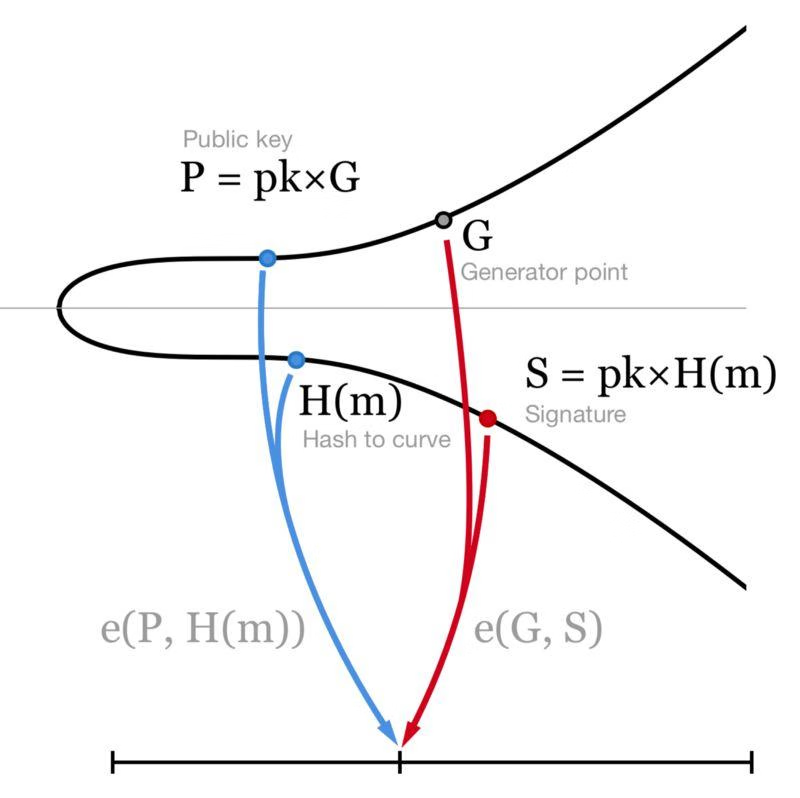
下图能够很直观的表示。BLS 签名验证,我们只需验证 公钥和消息的哈希值(曲线上两个点)与曲线生成点和签名(曲线上另两个点)是否映射到同一个数(若是则说明这是一个有效的 BLS 签名)。
四、签名聚合
前面提到BLS签名算法可以实现签名聚合,下面就来介绍这个非常棒的特性。
现在假设在区块链的场景下,有一个区块有1000笔交易,每笔交易都由 签名Si、公钥Pi 和 消息mi 组成。现在我们只关心区块中所有的签名(而不是每一个)是否正确。为获得聚合签名,只需要将区块中的所有签名加起来:
S=S1+S2+...+S1000
为了验证该区块是否正确,要保证下面这个等式成立。
e ( G , S ) = e ( P1 , H(m1) ) × e ( P2 , H(m2) ) × ... × e ( P1000 , H(m1000) )
如果签名是有效的,那么该等式是成立的。证明如下:(这里我直接放word里的截图)
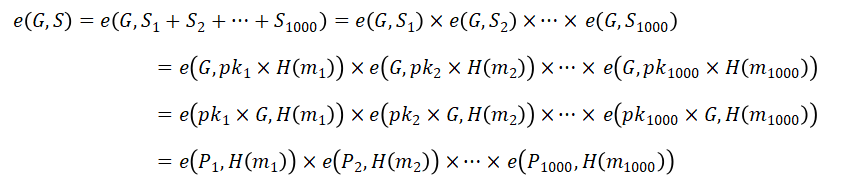
这里我们仍需用到所有的公钥,并计算 1001 次配对函数,好处是,区块中的签名只占 33 字节了。签名聚合可以由矿工在挖矿时完成,节省大量的区块空间。
4.1 n-n多重签名
使用多重签名的地址时,我们会对同一笔交易用不同的密钥进行签名。这种情况下,可以和 Schnorr 算法一样使用聚合密钥,把所有密钥和签名聚合成单个公钥和签名。
下面我们以 3-3 多重签名方案为例(同理可推导任意数量的多重签名方案)。一种简单的聚合方法,是把所有的签名和密钥加起来即可。即:
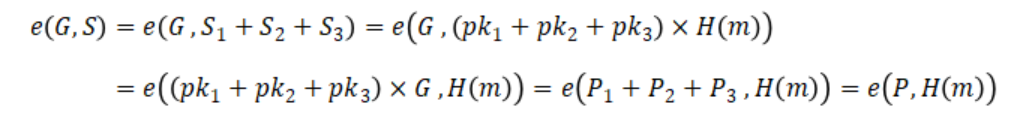
和 Schnorr 一样,我们也需要杜绝伪造密钥攻击。一种方法是要求每个签名参与者证明它拥有公钥对应的私钥(用私钥给公钥签名)。另一种方法是加入非线性系数,使得攻击无法实施。要做到这一点,聚合不再是简单的将多个密钥和签名相加,而是将它们分别乘以某个系数后再相加:
S = a1 × S1 + a2 × S2 + a3 × S3
P = a1 × P1 + a2 × P2 + a3 × P3
公式中签名和密钥的系数,可以通过签名者以及其它所有人的公钥计算得出,公式如下:
ai = hash (Pi, {P1, P2, P3})
举个例子,可以简单的将签名者的公钥和所有人公钥拼接在一起算出系数:
ai = hash (Pi || P1|| P2 || P3)
此时,上面的验证公式依然成立。虽然多了系数ai,但计算逻辑未变。
该方案的好处是,无需在设备间进行多轮通信,只需知晓其它签名者的相应信息即可。它可比 Schnorr 算法(需要 3 轮通信)的多重签名方案简单多了。这个方案也不依赖随机性,是一种具有完全确定性的签名算法。
4.2 m-n多重签名
上面对n-n多重签名进行了介绍,但实际中其实并不是很常见,更常用的是m-n多重签名。
Schnorr 签名算法中,我们用公钥组成的默克尔树来实现密钥聚合,这种方式效率不高,但是将将堪用。不幸地是,当 m 和 n 的值变大时,默克尔树的大小会呈指数增长。
BLS 使用了另一种方法,不过略复杂。我们需要一个普通哈希函数hash(x)(结果为一个数)和一个曲线哈希函数H(x)。开始多重签名时,还需要一个初始化过程,这之后,签名者之间就不再需要通信了,只需提供交易签名即可。
下面举个例子,我们要创建一个 2-3 多重签名,3 个签名存储在不同的设备上(这个例子可以扩展为任意的 m-n 多重签名)。
(1)生成成员密钥
用 i = 1,2,3 来表示集合中相应位置的设备,用pki表示私钥,用Pi = pki×G表示公钥。我们用前面说的方法来聚合公钥:
P = a1 × P1 + a2 × P2 + a3 × P3
其中,ai = hash (Pi, {P1, P2, P3}) .
现在,每个设备都需要对每个i签名,以证明该i是聚合公钥中的一员。将签名聚合后,保存在对应的设备中:
MKi = (a1 × pk1) × H( P , i ) + (a2 × pk2) × H( P , i ) + (a3 × pk3) × H( P , i )
这个签名被称作“成员密钥”,稍后签名时我们会用到。每个成员密钥都是对消息体H( P , i ) 的 n-n 多重签名,即:
e (G, MKi) = e (P, H(P , i) )
证明如下:
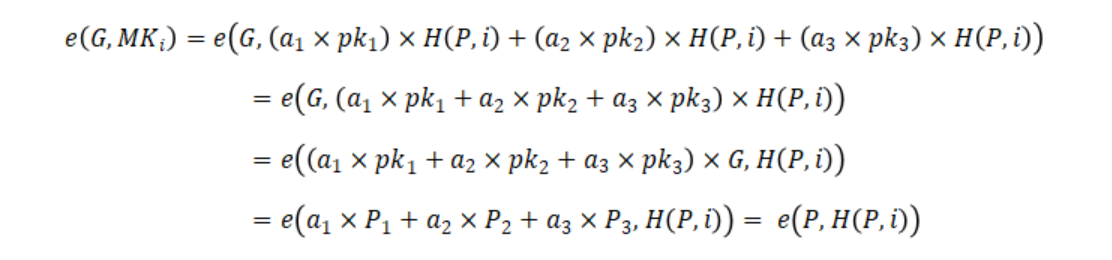
记住这个等式,稍后还会用到。它用来证明某个设备是多重签名中的合法参与者。
(2)签名
假设现在用pk1和 pk3对交易进行签名,会生成两个签名S1和S3:
S1 = pk1 × H(P,m) + MK1
S3 = pk3 × H(P,m) + MK3
将它们加起来,聚合成单一的签名和公钥:
(S', P') = (S1+S3, P1+P3)
用P'和S', 是为了强调它们只是由部分签名者参与计算的(公钥和签名),而不像 P 那样是由所有签名者参与计算的(公钥)。为了验证 2-3 多重签名,需证明如下等式成立:
e(G,S') = e(P',H(P,m)) × e(P,H(P,1)+H(P,3))
上面说过,成员密钥 MK1 和 MK3 是对消息 H(P,1) 和 H(P,3)(消息本身由聚合公钥P签名)的签名,所以有:
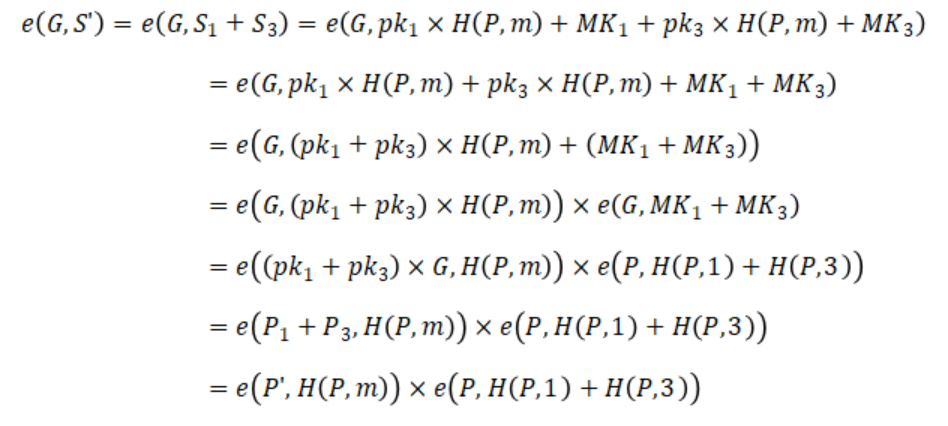
证明完毕。比 n-n 多重签名复杂一些,但仍然可以理解。
五、缺点
① 配对函数并不是十分高效
② 存在一种针对椭圆曲线加密体系的攻击-MOV攻击。该攻击能够利用配对函数来危害系统安全。所以对配对函数的使用要十分谨慎。
参考文献
[1] Boneh D , Lynn B , Shacham H . Short Signatures from the Weil Pairing[J]. Springer, Berlin, Heidelberg, 2001.
[2] 理解 BLS 签名算法

留言评论