[算法2-数组与字符串的查找与匹配] (.NET源码学习)
关键词:1. 数组查找(算法) 2. 字符串查找(算法) 3. C#中的String(源码) 4. 特性Attribute 与内在属性(源码) 5. 字符串的比较(底层原理) 6. C#中的StringComparsion(源码) 7. 字符串与暂存池(底层原理)
【注:本人在写文章时遇到认为有必要或想要展开的点就会将其并入文章中,避免事后遗忘。因此非主题内容可能会比较多,篇幅也可能比较大,各位学者在浏览时可以自行转跳到感兴趣的部分进行阅览,存在相关问题或建议,欢迎留言指导,谢谢!】
查找,大体上可以分为两类:数组查找、字符串查找。其中数组查找以二分为主;字符串查找以BK、BM、KMP三类算法为主。由于二分在之前的文章中已经详细叙述过,在此不再重复论述。故本文主要以有关字符串的查找为重点,附带.NET关于String类型及相关底层逻辑的源码分析为主,进行论述。
【# 请先阅读注意事项】
【注:
(1)文章篇幅较长,可直接转跳至想阅读的部分。
(2)以下提到的复杂度仅为算法本身,不计入算法之外的部分(如,待排序数组的空间占用)且时间复杂度为平均时间复杂度。
(3)除特殊标识外,测试环境与代码均为.NET 6/C# 10。
(4)默认情况下,所有解释与用例的目标数据均为升序。
(5)默认情况下,图片与文字的关系:图片下方,是该幅图片的解释。
(6)文末“ [ # … ] ”的部分仅作补充说明,非主题(算法)内容,该部分属于 .NET 底层运行逻辑,有兴趣可自行参阅。
(7)本文内容基本为本人理解所得,可能存在较多错误,欢迎指出并提出意见,谢谢。】
一、有关数组
(一) 二分查找及相关优化
关于二分的相关内容,在本人的这篇文章中(LC T668笔记 & 有关二分查找、第K小数、BFPRT算法 - PaperHammer - 博客园 (cnblogs.com))有较为详细地论述,详情请参阅。
在此,仅总结一下二分的要点:
1. 二分集合须保证有序。有序是二分的前提,在二分前须明确二分的对象,该对象必须具有有序性。
2. 确定搜索区间形式(闭区间、左闭右开、左开右闭)。不同区间形式,循环条件与最终返回值不同;同时也应用于不同的场景。
3. 尽量写或想清楚所有的if…else…,清楚地展现出所有细节,避免不必要的纰漏与麻烦。
(二) 有关方法BinarySearch()的源码
该方法的主要实现形式是双指针或折半查找,详细内容在本人之前的文章([数据结构1.2-线性表] 动态数组ArrayList(.NET源码学习) - PaperHammer - 博客园 (cnblogs.com))中,详情请参阅。
二、有关字符串
(一) .NET中的String与C#中的string
1. C#是区分大小写的语言,所以string与String理论上是不同的,但在编译器的定义导航中,却将这两个类型均导航至同一个类——类String。
2. 据现有资料可知,String是.NET(以前称为.NET Framework)中的类,string是C#中的类。在C#中使用string时,编译器会将string自动映射到.NET中的String,同时调用的方法也是.NET中类String内部的方法。据该原理,使用String可以在一定程度上减少编译器的工作量,但微软官方不建议这样,依旧建议使用string以符合相关规范。其他基本数据类型也是如此,如short映射Int16,int映射Int32,long映射Int64,double映射Double等。
3. 这样做的原因个人猜测可能如下:.NET是一套底层运行规范,其需要对所有支持的语言定义一个通用的规则(CLS通用语言规范Common Language Specification)不同语言语法的不同,.NET通过CLS提供了公共的语法,不同语言经过IL的翻译生成对应的.NET语法。如F#中的let赋值语句(let str = “.NET”;;);VB中的String(Dim 变量名 As String = “.NET”);加上现在C#中的string。它们都是基于.NET运行的,所以需要有一个总纲来规范化,使得每个语言具有独特性的同时,可以实现相同或相近的功能。因此在.NET中定义了类String,无论时哪种语言,只要编译时需要使用.NET,均须遵守其相关规范,将独特的风格转换为统一且通用的规范化表达。
4. 因此,String不是C#中的关键字,可以将其用作变量名。
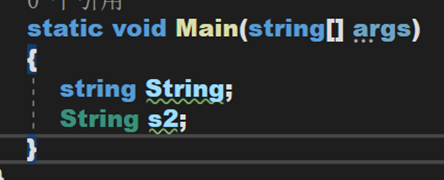
(二) 有关类String

String类位于命名空间System中,是一个公共密封类,继承了许多接口,其中“著名的”有:IComparable用于字符串间的比较;IEnumerable用于迭代器的遍历。其内部包含2个属性,3个字段,1个结构(体),3种运算符的重载方法,9个构造方法和一堆其他方法(真的太多了)。
1. 两个属性
首先是索引器,可以发现这是一个以int为索引,char为返回值的只读索引器。对比其他数据类型的索引器,如之前文章提到的动态数组ArrayList
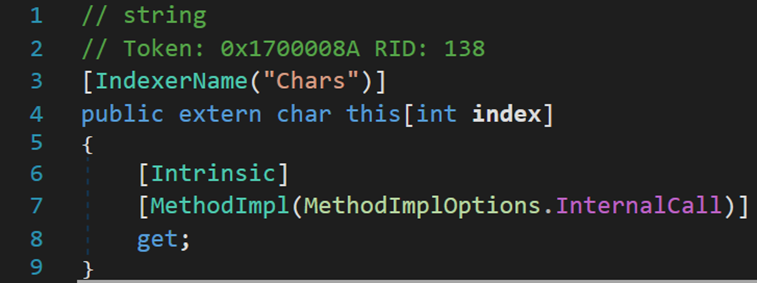
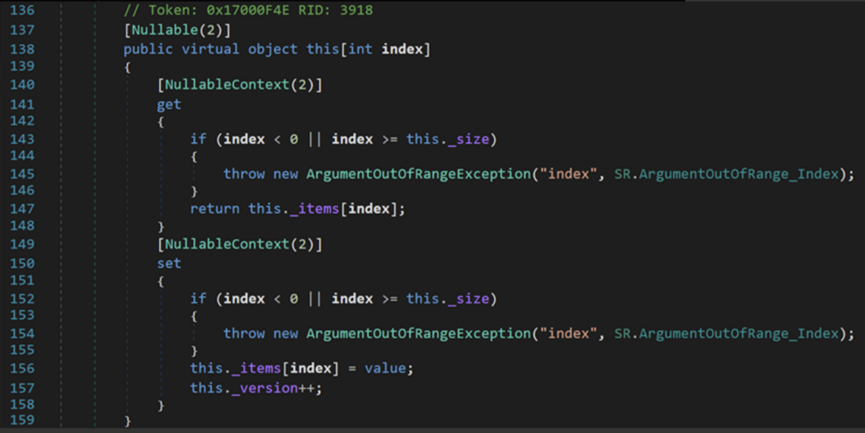
不难发现,String中的索引器只读不能写,因此经常头昏会写出这样的代码:
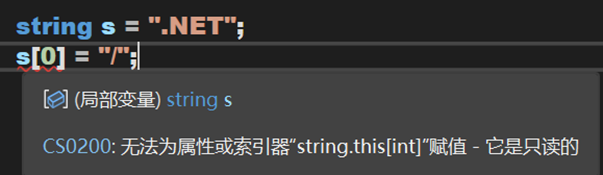
同时,String类中的索引器还是一个extern属性,说明其支持在外部根据不同的需求重新定义新的索引器。

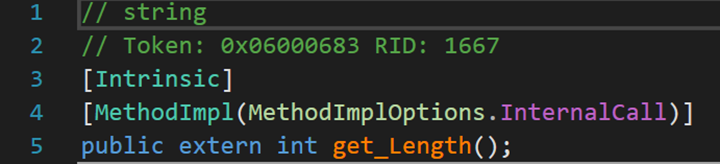
第二个数Length属性,其内部包含了一个get_Length()方法,用于返回字符串的长度(调用的时候,不用在后面加括号,且第一个字母大写)。
可以看到,这里都出现了Intrinsic和MethodImpl及其相关内容,这两个内容会在文末进行补充说明。
2. 三个字段
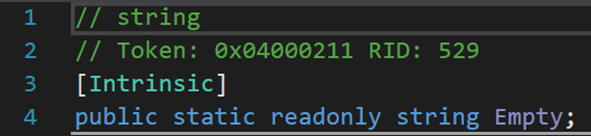
string.Empty用于初始化字符串为空。这里对四种初始化方式:(省略前缀string)str = null;str = “”;str = string.Empty;str = new()进行分析。
(1)对于str = null,理论上这种方式不能称之为常规意义上的初始化,因为赋值为null并没有在堆上分配,仅是在栈上分配了空间,依然不可直接使用,因为变量不引用内存中的任何对象。这种方式,相当于只定义了一个变量并未对其赋值,在使用前必须先赋值。
(2)对于str = “”与str = string.Empty,其初始化并在内存空间堆与栈上都进行分配,将其赋值为空。其在基本用法和性能上并没有较大差异。
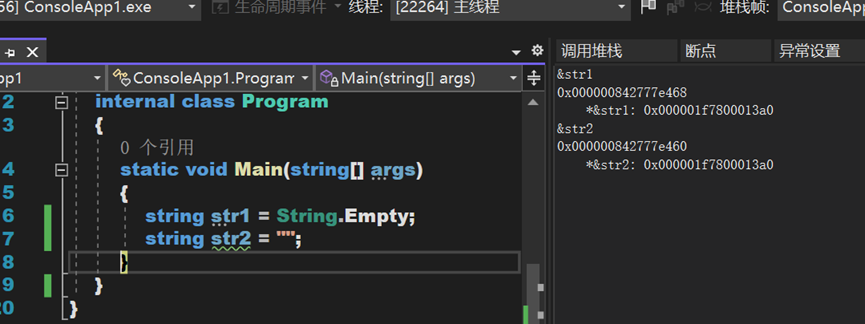
据测试后可知,即使已存在一个空字符串,用以上两种方法继续进行定义变量,均不会重新申请新的内存空间,而是每次去指向固定的静态只读内存区域。
据CLR中的相关信息及本人的理解,二者仅仅在优化方面稍有差别,string.Empty是C#对""在语法级别的优化。也就是说,""是通过CLR(Common Language Runtime公共语言运行库)进行优化的,CLR会维护一个字符串池,以防在堆中创建重复的字符串。而string.Empty是一种C#语法级别的优化,是在C#编译器将代码编译为IL(即MSIL)时进行了优化,即所有对string类的静态字段Empty的访问都会被指向同一引用,以节省内存空间。
还有两外两个字段。这两字段从命名来看,一个变量存储的是字符串的长度;另一个存储的是第一个字符。有关二者的应用及更多内容,会在之后的某些方法中进一步解释。
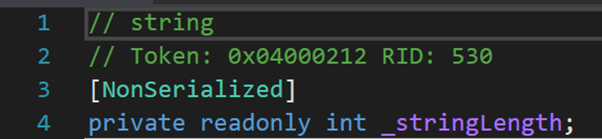
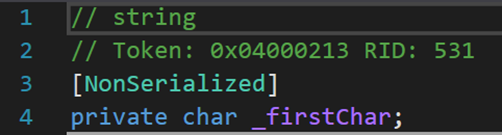
3. 一个结构(体)
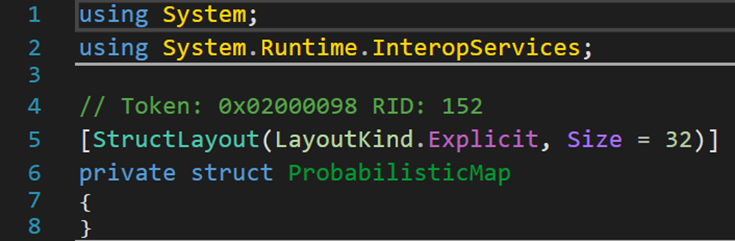
该结构体派生自类object下的类ValueType,从父类来看应该是用于存储某些数据类型间的映射关系。(下方翻译来自Microsoft Bing)
4. 三种运算符重载
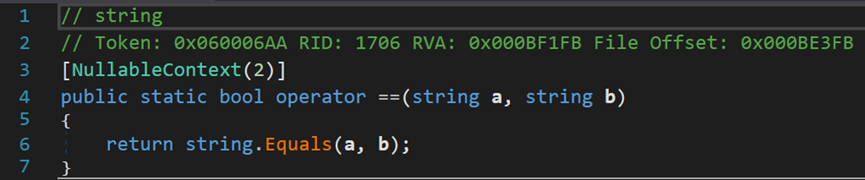
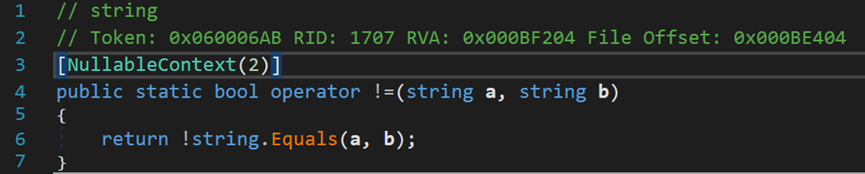

首先是运算符“==”和“!=”。对于两个字符串的比较,类String内部从新定义了比较规则,即重载了判断运算符,使用判断运算符就相当于调用类String内部的Equals()方法。因此,对于字符串而言,使用“==”和方法Equals()进行比较,是完全等价的。
一般地,对于运算符“==”和Equals()方法,在比较方式上还是有所差异。
(1)对于值类型和字符串,这两种方式均只比较内容;
(2)对于除字符串以外的引用类型,运算符”==”比较的是在栈中的引用(是否指向同一个对象);方法Equals()比较的是在堆中的内容(是否是同一个对象的引用)。
但这样就有一个问题,我们知道C#对于字符串有某些优化。一般地,内容相同的字符串不会开辟新的堆空间,而是指向储存在暂存池(堆的一部分,Java中称为常量池)中的对象。但以某些方式创建的字符串对象,并不会检查暂存池,而是直接在堆中开辟新空间,导致内容相同的字符串,栈和堆的地址均不同。那么这样是否会导致判断运算符和方法Equals()出现问题呢?有关该部分的详细内容请转到文末的 [# 有关字符串的比较与暂存池]
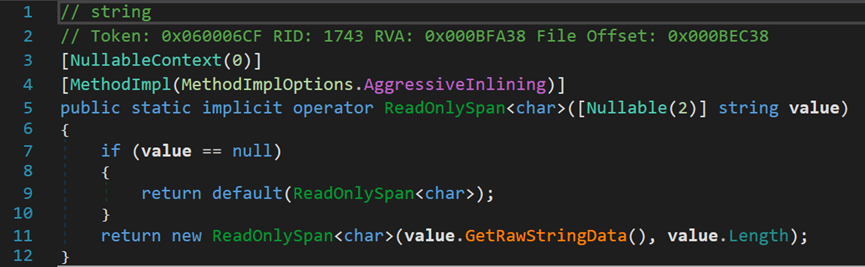
其次是ReadOnlySpan<T>。这是一种较为特殊的运算符重载,其中关键字implicit用于声明隐式的自定义类型转换运算符。它可以实现2个不同类型的隐式转换,提高代码的可读性。但是使用隐式转换操作符之后,在编译时会跳过异常检查,所以在使用隐式转换运算符前,应当在一定程度上确保其不会引发异常并且不会丢失信息,否则在运行时会出现一些意外的问题。该隐式转换,是将string类型转换成ReadOnlySpan<char>类型。
先简单介绍一下类型Span<T>

该类型被微软官方称为“新增的重要组成部分“,其主要作用是提供任意内存连续区域的类型安全与内存安全表示形式。即,此数据类型可以实现对任意内存的相邻区域进行操作,无论相应内存是与托管对象相关联,还是通过互操作由本机代码提供,亦或是位于堆栈上。解决了在不使用不安全代码(指针等直接对内存进行的操作)的情况下,实现了在内存上,对数据进行修改的操作。更多详细信息请参阅(C# - Span 全面介绍:探索 .NET 新增的重要组成部分 | Microsoft Docs)。
ReadOnlySpan<T>亦是如此,只是被附上了对内部元素只读的属性,以满足字符串不可修改的基本性质。


其将传入的字符串首字符作为指针的起始位置,length为字符串的长度,通过指针+偏移量的方式(类似于C++中通过指针ptr访问数组第一个位置,ptr++实现向后偏移),实现对数据的访问。
5. 九个构造方法
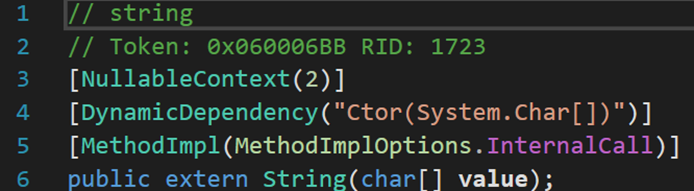
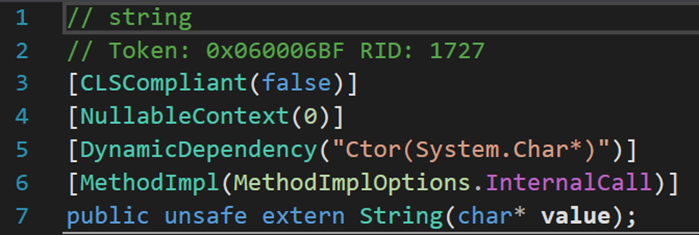
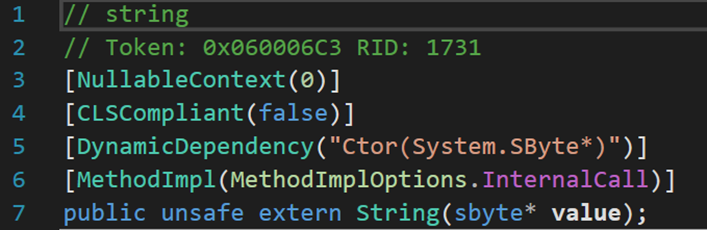
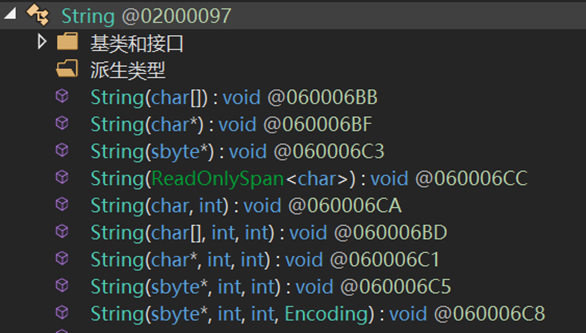
与其他类型的构造方法不同,这九个构造方法均为外部方法extern,需要从外部从新定义其实现形式。个人猜测,外部定义可能在.NET库中。其功能均是将所给数据集,按照一定条件转化为字符串。详细信息参考下表:
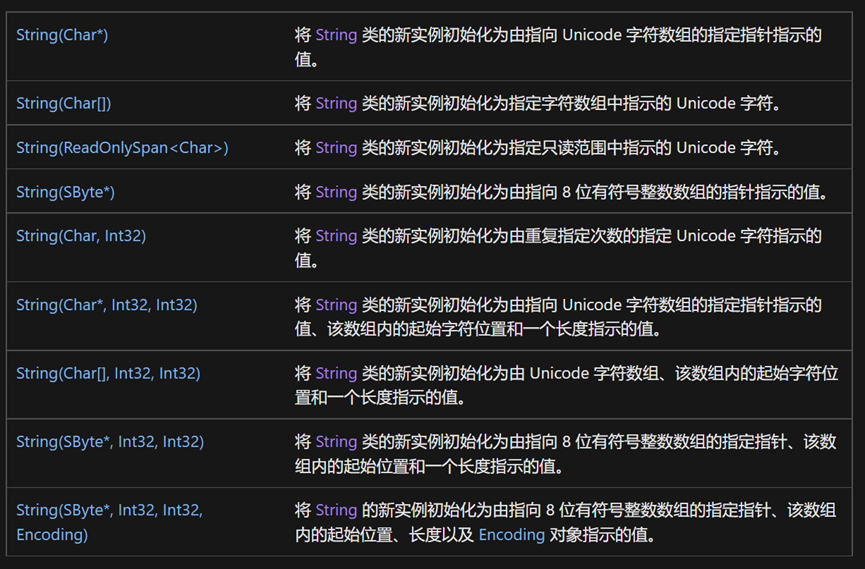
(三) 有关String的查找与匹配
1. BF算法(Brute Force)
Brute Force,一种暴力匹配算法,其思想是对于两个字符串 s 与 ,在s(主串)中查找/匹配pat(模式串)。若s[i] == pat[j],则i++且j++;否则i++且j = 0。此时 i 即为模式串 pat 在主串 s 中第一次匹配的起始下标位置。
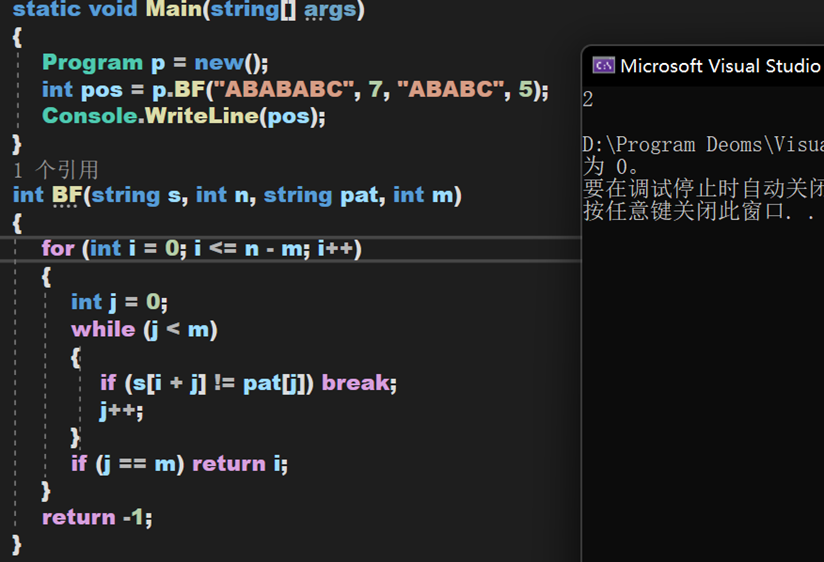
复杂度分析:
- 时间复杂度:O( nm )(最快O( n+ m ),pat 在 s 的开头就匹配完成;最慢O( nm ),每次都是在 pat 的末尾匹配失败)
- 空间复杂度:O( 1 )
我们找个题目测试一下其运行效率(题目:kmp算法_牛客题霸_牛客网 (nowcoder.com))

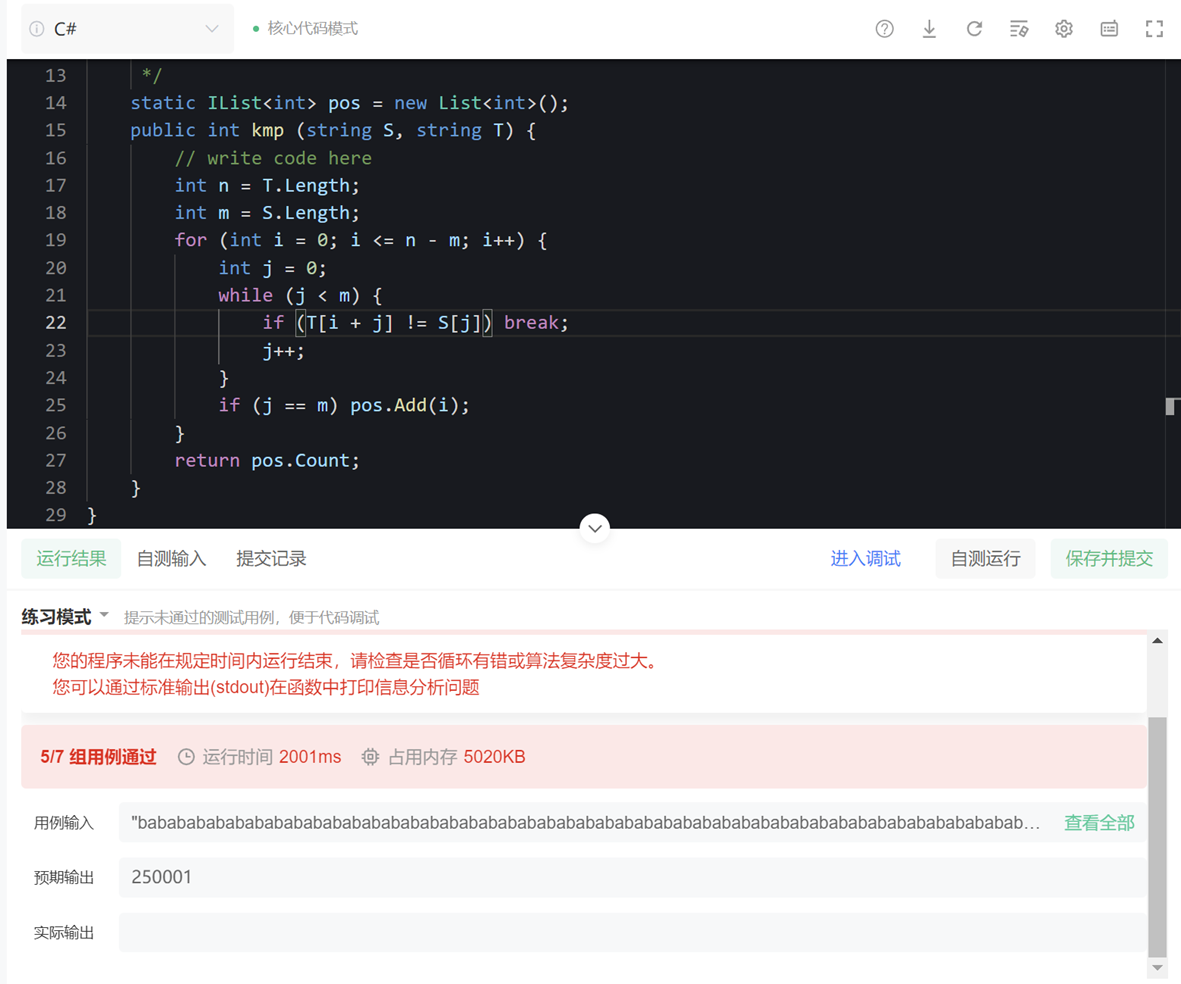
实测运行时间:
【注:由于牛客上的本题无法获取该超时样例,因此此处及之后选用某一衰减测试样例进行实测计时,仅用于观察算法时间复杂度。样例:主串字符全为 ‘A’,长度为500000;模式串字符全为 ‘A’,长度为100】
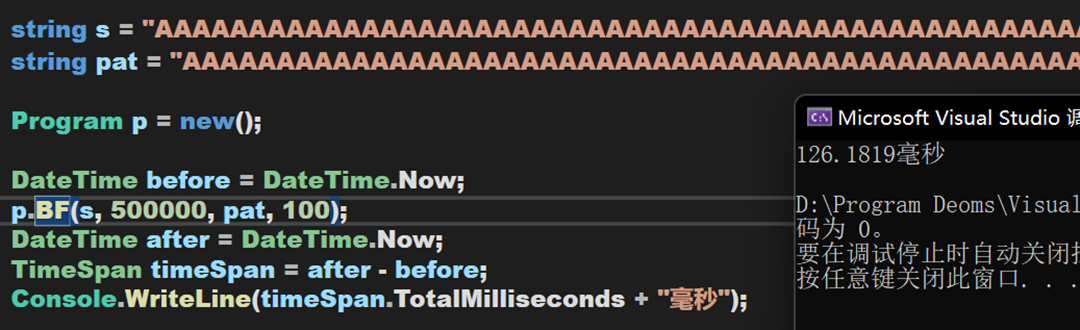
毫无疑问,对于这样的时间复杂度, 105 及以上量级的数据是比较慢的。虽然理论上BF算法时间复杂度较高,但其在实际开发中比较常用原因主要有以下2点:
(1)实际开发中,多数情况下主串与模式串长度不会很长。对于小规模数据,其时间复杂度并不能代表其执行时间,某些情况下,可能比其他优化后的算法更快。因此,尽管理论最坏时间复杂度为 O( nm ),但从概率统计上看,多数情况下其效率还是可观的。(打比赛另说)
(2)BF 算法思想简单,实现简单。简单意味着不容易出错,出错也很容易查找修改。工程应用中,在满足性能的前提下,简单是我们的首选。这也符合 KISS (Keep It Simple and Stupid) 设计原则。
【思考】如果要返回所有匹配的字串首地址,该如何实现?
【参考如下】
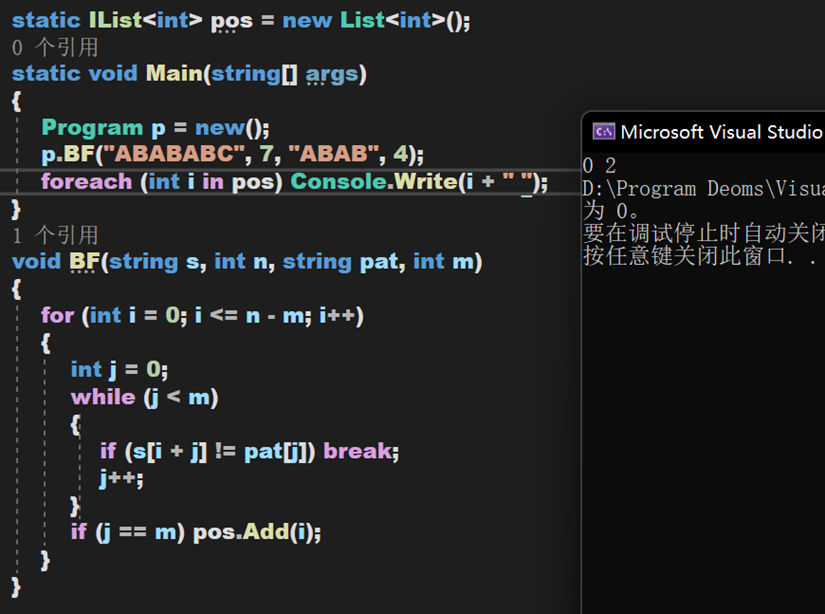
2. RK算法(Rabin-Karp)
该算法算是对BF算法的优化,既然比较字符效率不高,那不如换一种比较对象。要转换那就需要保证按照某种规则进行转换,且转换后需要保证唯一性。对于每个字符串,除了它本身外有一种一般情况下唯一的表示方式,哈希值。并且数字的比较效率要比字符高上不少;而且字符要一个一个比较,而哈希值可以代表一个串,所以比较的时候时间复杂度为 O( n )。
简单来说其方法思想是,在主串中每次截取和模式串一样长的字符串,获取二者的哈希值进行比较。
【注:有关.NET/C#中的哈希及其冲突的问题,会在今后的文章的提到,以下均默认不会发生哈希冲突】
获取哈希值有两种方法:
(1)遍历字串中每个字符。这样就会有许多操作:截取、遍历、计算。但反复直接截取并没有优化时间复杂度,反而在一定程度上增加了时间复杂度,因为截取字符串也是一个O(n)级的操作,因此总时间复杂度依旧是O(n2)级。我们好不容易将复杂度降低了一个量级,结果算个哈希又把量级升了回来,得不偿失。
(2)滑动窗口。
根据滑动窗口的原理,获取第一个串后,之后串的哈希值,可以根据移除前一个,加入后一个来实现,从而将O(n)的时间复杂度降为O(1)。具体实现如下:
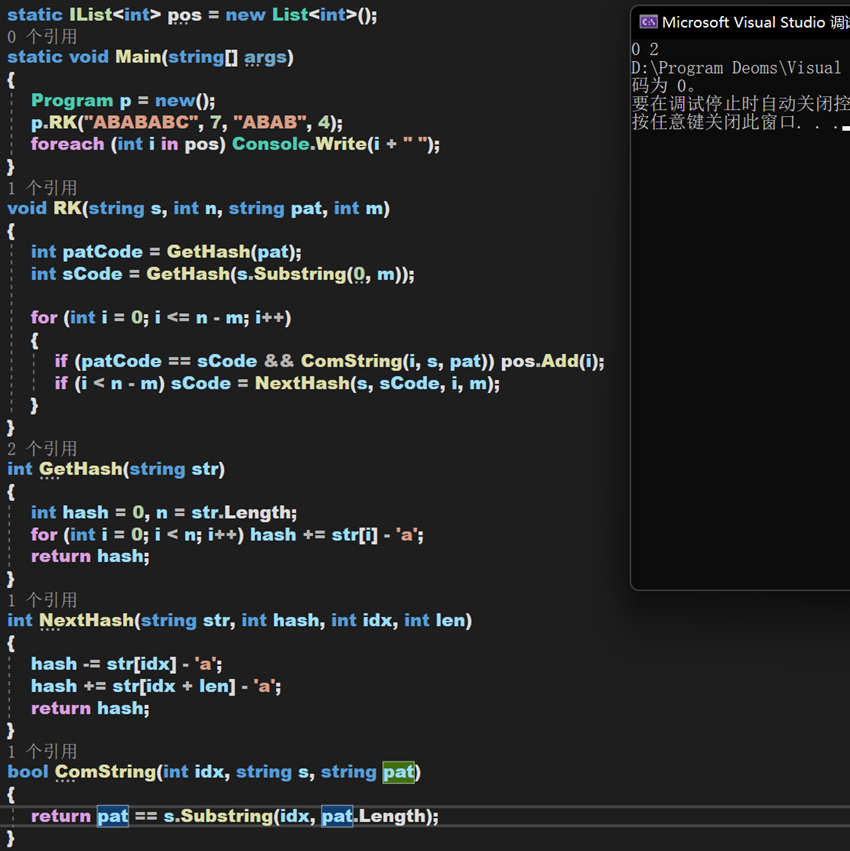
复杂度分析:
现在,该算法第一次计算t的哈希值时,时间复杂度为O( n );后续计算哈希值因为利用了滑窗的优化只有O( 1 );比较字符串的Equals()方法,一般地,可以视为O( 1 )。
- 总时间复杂度为O( n )
- 空间复杂度为O( 1 )
这里解释一下为什么两串求得的哈希值相同还要对字符串本身进行比较。当两个串字符类型与数量相同时(如 “aaab”,”abaa” )以这样的方式进行哈希计算,会得出相同的值,但两个字符串本身并不相同。这也是其缺点:不稳定,过于简单的计算方式或较大的数据量很容易产生哈希冲突。同时,在极端情况下,如果存在大量哈希冲突(哈希值相同,字符串本身并不相同),每次都要比较主串某一部分与模式串,那么RK算法就会退化为BF算法,时间复杂度重回 O( nm )。
同样,再测一下刚才的题
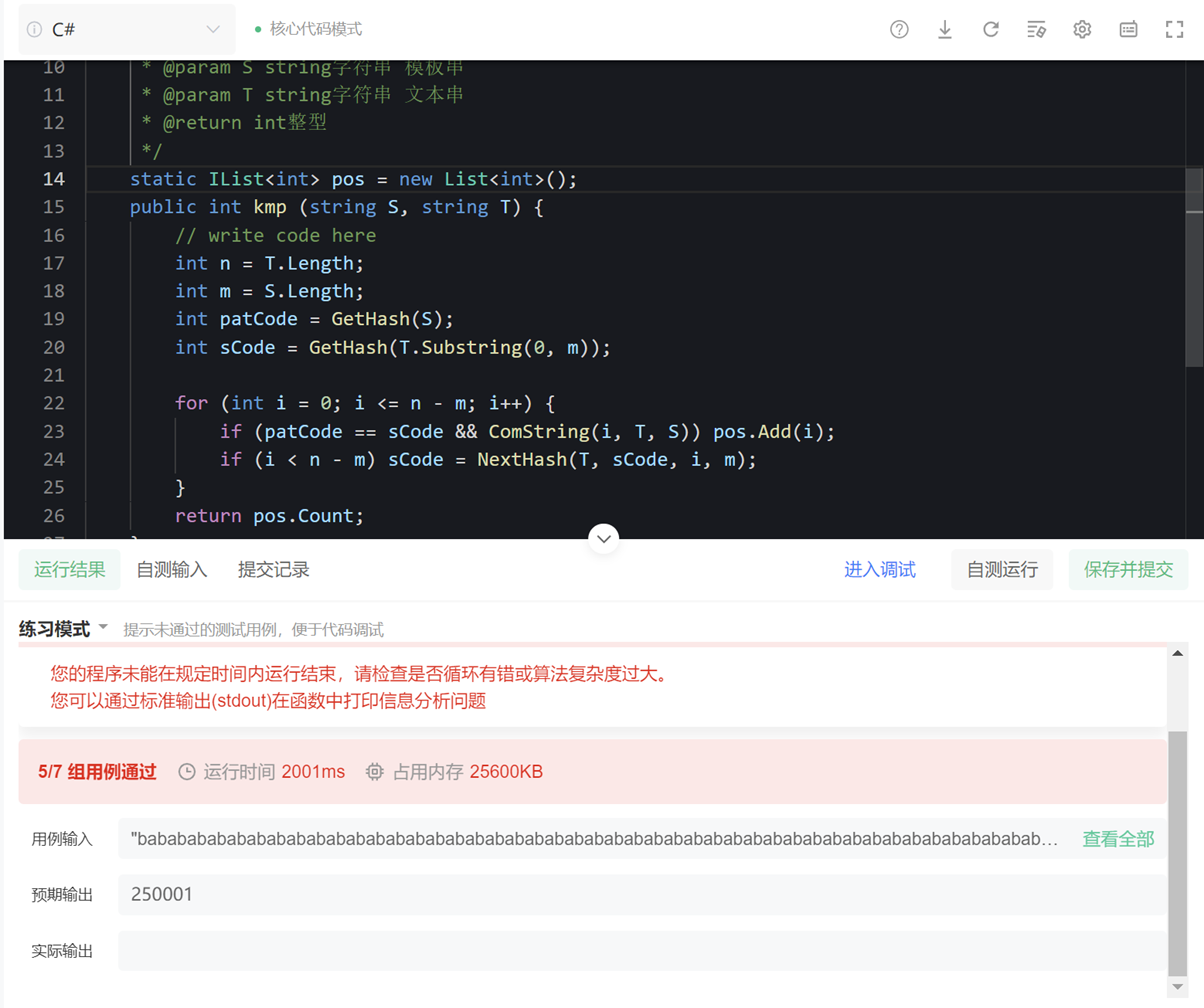
实测时间:
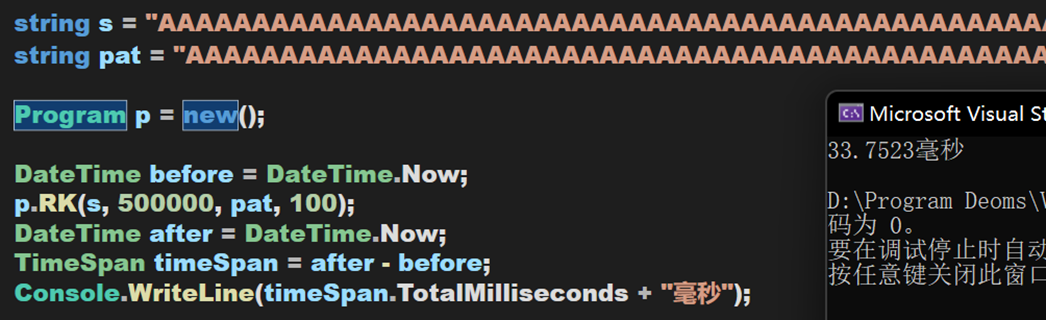
可以发现,RK算法在一定程度上确实比纯暴力得BF算法效率要高,尤其是当主串长度越长时,提升越明显。
【思考】假设有两个以行为优先主序列二维矩阵,如果要返回所有匹配的字串首地址,该如何实现?
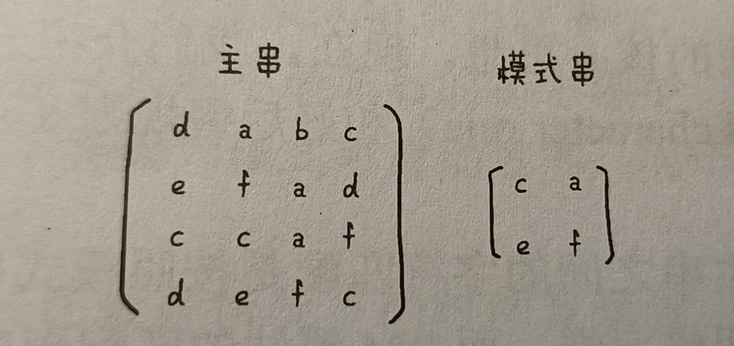
【参考如下】
RK算法比较的是字符串的哈希值,那只要获取了对应位置的哈希值,进行比较即可。对于一维,在哈希值转移时只需减去前一个、加上后一个;而二维的转移需根据模式串的规格而定。
using System;
using System.Collections;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Numerics;
using System.Diagnostics;
using System.Runtime.CompilerServices;
namespace Common
{
internal class Program
{
static IList<int[]> pos = new List<int[]>();
static int m, n;
static int p, q;
static void Main(string[] args)
{
Program pg = new();
char[][] s = {
new char[]{ 'c', 'a', 'b', 'c' },
new char[]{ 'e', 'f', 'a', 'd' },
new char[]{ 'c', 'c', 'a', 'f' },
new char[]{ 'd', 'e', 'f', 'c' }
};
char[][] pat = {
new char[]{ 'c', 'a' },
new char[]{ 'e', 'f' }
};
m = s.Length;
n = s[0].Length;
p = pat.Length;
q = pat[0].Length;
pg.RK(s, pat);
foreach (int[] arr in pos) Console.WriteLine("{ " + arr[0] + ", " + arr[1] + " }");
}
void RK(char[][] s, char[][] pat)
{
int patCode = GetHash(pat, 0, 0);
int sCode = GetHash(s, 0, 0);
for (int row = 0; row <= m - p; row++)
{
for (int col = 0; col <= n - q; col++)
{
if (patCode == sCode && ComString(s, pat, row, col)) pos.Add(new int[] { row, col });
if (row < m - p || col < n - q) sCode = NextHash(s, sCode, row, col);
}
}
}
int GetHash(char[][] tmp, int row, int col)
{
int hash = 0;
for (int i = row, cntR = 0; cntR < p; i++, cntR++)
for (int j = col, cntC = 0; cntC < q; j++, cntC++)
hash += tmp[i][j] - 'a';
return hash;
}
int NextHash(char[][] s, int hash, int row, int col)
{
if (row < m - p && col == n - q) return GetHash(s, row + 1, 0);
for (int i = row, cntR = 0; cntR < p; i++, cntR++)
{
hash -= s[i][col] - 'a';
hash += s[i][col + q] - 'a';
}
return hash;
}
bool ComString(char[][] s, char[][] pat, int row, int col)
{
for (int i = row, cntR = 0; cntR < p; i++, cntR++)
for (int j = col, cntC = 0; cntC < q; j++, cntC++)
if (s[i][j] != pat[cntR][cntC]) return false;
return true;
}
}
}
3. KMP算法(Knuth-Morris-Pratt)
【参考文章:漫画:什么是KMP算法?;KMP算法—终于全部弄懂了_June·D的博客-CSDN博客】
回顾一下前两种算法效率不高的原因:在不匹配时,从待匹配串的起始位置重新全部开始匹配;反复计算哈希值,且需要处理哈希冲突的问题。这两种方式可以看作每次将字符串向后一位一位滑动。这样的方式导致了中间存在大量无意义的比较,以及不得不完成的比较,使得效率低下。而KMP就针对这一点进行了优化,其核心在于:在匹配过程中,当不匹配时,对于已匹配好的部分,找到一种规律,将模式串一次性向后滑动很多位,从而提高效率。其中,记不匹配的字符为 “坏字符”,已匹配的部分为 “好前缀”。
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 于是现在的问题就:如何制定滑动策略?
思考一个应用场景:在一篇文章中匹配某个字符串。那么对于不同的主串,总是用同一个模式串去匹配。如果每针对一个新匹配的主串都要制定新的策略,那么时间复杂度依旧是 n2 级,甚至超过该级数。因此,制定的滑动策略不应该依赖于主串,对于同一个模式串,应当尝试制定同一个滑动策略。即,滑动的策略只与模式串有关。
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 接下来进一步思考滑动策略的细节:不匹配时,应当滑动到哪里?
举个例子:
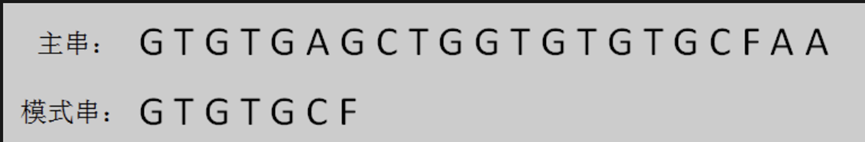
首先,把主串和模式串的首位对齐,从左到右对逐个字符进行比较。
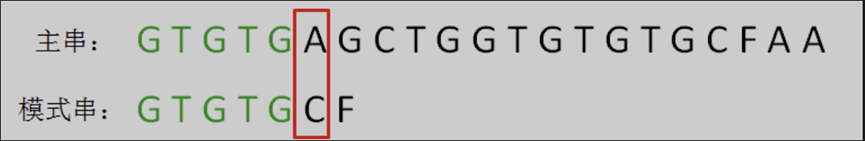
第一轮,发现前5个字符都是匹配的,第6个字符不匹配,将其标记为坏字符 ‘A’。

【重难点】
可以发现,在好前缀 “GTGTG” 当中,主串的好前缀的后三个字符 “GTG” 和模式串的前三位字符 “GTG” 是相同的。我们分别把这两部分记作可匹配后缀子串与可匹配前缀子串。在之后的比较中,这两部分一定能够匹配上。并且在这两个部分匹配上之前,一定没有其他可能使得模式串成功匹配的情况,这也为选择最长的子串进行滑动提供了保障。因此,我们直接将模式串后移两位,使得这两部分对齐,并开始下一次比较,省去了中间的无效比较。
同理,如果在好前缀中如果存在多个可匹配后缀子串,那么为了能省区更多的无效比较,我们选择找到最长的子串进行滑动。因此,我们的滑动策略为:在主串的好前缀中,找到最长可匹配后缀子串;在模式串中,找到对应的最长可匹配前缀子串。
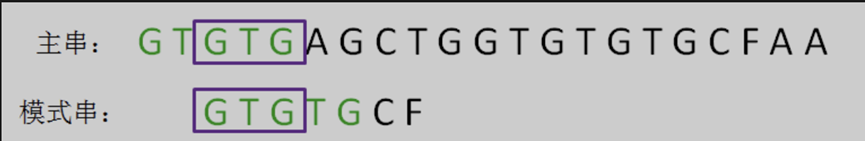
第二轮,我们直接把模式串向后移动两位,让两个 “GTG” 对齐,继续从刚才主串的坏字符 ‘A’ 开始进行比较。

此时,主串的字符 ‘A’ 仍然是坏字符,这时候的匹配前缀缩短成了 “GTG”。

按照第一轮的思路,我们来重新确定最长可匹配后缀子串和最长可匹配前缀子串。此时,剩下字符串 “G”。

第三轮,我们再次把模式串向后移动两位,让两个“G”对齐,继续从刚才主串的坏字符A开始进行比较。
……
小结:整体思路是,在主串的好前缀中寻找最长可匹配后缀子串(在好前缀中,从后往前找),在模式串中寻找对应的最长可匹配前缀子串(在已匹配串中,从前往后找),直接把两者对齐,从而实现模式串的快速滑动。
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 知道了退回到哪里,现在的关键在于如何实现退回?【重难点】
我们肯定不能每次都从头遍历一遍去寻找前后缀子串。前文提到找到某种规律,在每次失配后,都不会从头重新开始枚举,而是根据这种规律,从某个特定的位置开始匹配;而对于模式串的每一位,都具有唯一的规律,这种规律可以帮助我们利用已有的数据不用从头匹配,从而节约时间。
注意到,对于主串中的某一最长可匹配后缀子串,在当前状态下是已经匹配上的。如果在模式串中找到了另一个合法的最长可匹配前缀子串,那我们就将其进行滑动。说明,如果可以滑动,那么在模式串中,一定存在两个不同起始位置的子串,且这两个子串的内容是相同的。因此我们可以用这个信息,在只依赖模式串的情况下完成规律的查找与构建。
数学化表达:对于模式串 t 的每个元素 t[j],都存在一个实数 k ,使得模式串 t 开头的 k 个字符( t[ 0 ], t[ 1 ],…, t[ k-1 ] )依次与 t[ j ] 前面的 k 个字符( t[ j-k ], t[ j-k+1 ],…, t[ j-1 ] ) 相同(其中,字符 t[ j-k ] 最少从 t[ 1 ] 开始,须保证不重复,所以 k < j )。。如果这样的 k 有多个,则取最大的一个,以此保证最长。模式串 t 中每个位置 j 的字符都适配这种规律,定义一个 next 数组存储这种规律,即 next[ j ] = MAX{ k }。
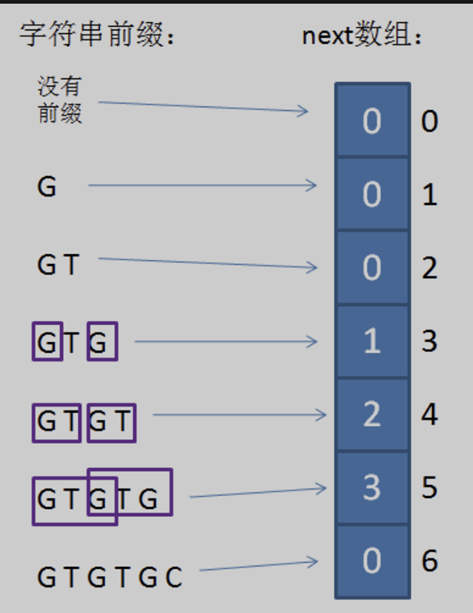
对于 next 数组,其索引表示当前比较的两个字符的位置 ‘j’ ;索引对应值表示 k 。若当前字符为坏字符,则可以滑动 j – k 位,即下一次的比较位置。
(1) 当模式串的第一个字符和主串不匹配时,并不存在已匹配前缀子串,更不存在最长可匹配前缀子串,因此next数组下标是0,next[ 0 ]的元素值也是0。
(2) 如果已匹配前缀是 “G”、“GT”、“GTGTGC”,但其并不存在最长可匹配前缀子串,所以对应的next数组元素值(next[ 1 ],next[ 2 ],next[ 6 ])同样是0。
(3) 对于好前缀 “GTG”,此时比较位置为索引 j = 3,从该位置向前找最长可匹配前缀子串;从开头找最长可匹配后缀子串,得出最长可匹配前缀是 ‘G’,即 k = 1(此时滑动 j – k = 2 位)。因此,对应数组中的next[ 3 ],元素值是k = 1(即,下一次的比较位置)。以此类推,“GTGT” 对应 next[ 4 ],元素值是2;“GTGTG“ 对应 next[ 5 ],元素值是3。
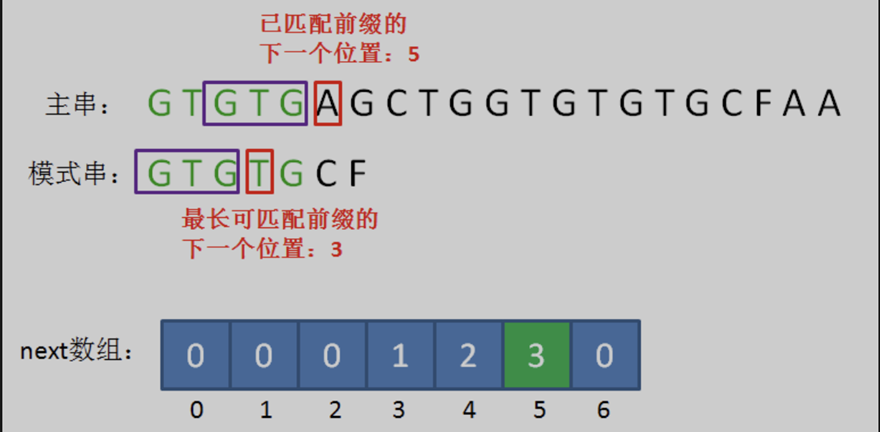
小结:用一个数组保存每个字符的信息,当在该字符处不匹配时,通过数组保存的信息,退回到相应位置。其中,数组的下标表示“当前比较两个字符的位置 j”,元素的值则是“最长可匹配前缀子串的下一个位置 《=》 最长可匹配前缀子串的长度 《=》 MAX{ k }”。
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 如何构建next数组?【重难点】
这个问题其实刚刚已经基本讲述清楚了,现在按照例子再过一遍,掌握这个构建方法,就掌握了KMP的核心。
由于已匹配前后缀子串仅在模式串中查找,与主串无关。所以仅依据模式串,即可生成next数组。
最简单的方法是从最长的前缀子串开始,把每一种可能情况都做一次判断。假设模式串的长度是m,生成next数组所需的最大总判断次数是1+2+3+4+......+m-2 次。
显然,这种方法的效率非常低,整体近似 n2 的量级。因此,可以采用类似“动态规划”的方法。首先next[ 0 ]和next[ 1 ]的值肯定是0,因为不存在前后缀字串;从next[ 2 ]开始,next数组的每一个元素都可以由上一个元素推导而来。
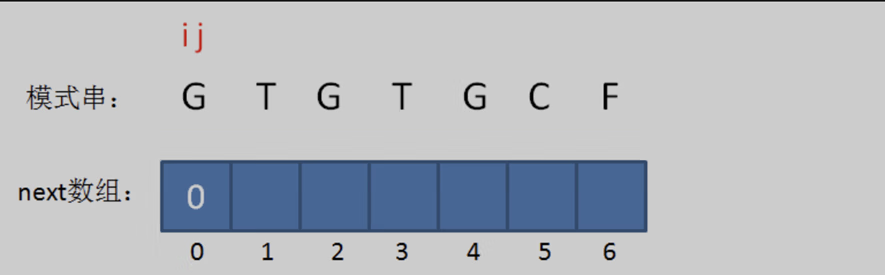
设置两个变量i和j,其中i表示“当前比较两字符的位置”,也就是待填充的数组下标;j表示“最长可匹配前缀子串的下一个位置”,即转跳回来的下一次比较位置,也就是待填充的元素值。分析可知,此时最长可匹配前缀子串不存在,所以当 i = 0 时,j = 0,next[ 0 ] = 0。

继续向后移动当前比较的位置。此时存在字符串 “G“,由于只有一个字符,不满足 k < j 的条件。因此,同样不存在最长可匹配前缀子串,所以当 i = 1 时,j = 0,next[ 1 ] = 0。

此时的已匹配前缀是 “GT”,由于模式串当中 pat[ j ] != pat [ i-1 ],即’G’ != ‘T’,最长可匹配前缀子串仍然不存在。所以当 i = 2 时,j = 0,next[ 2 ] = 0。
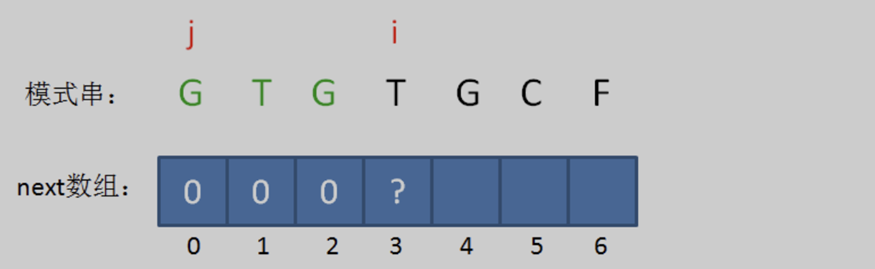
继续后移。此时的可匹配前缀是 “GTG“,此时模式串中 pat [ j ] == pat [ i-1 ],即 ‘G‘ = ’G‘,最长可匹配前缀子串出现了,是 ”G“。
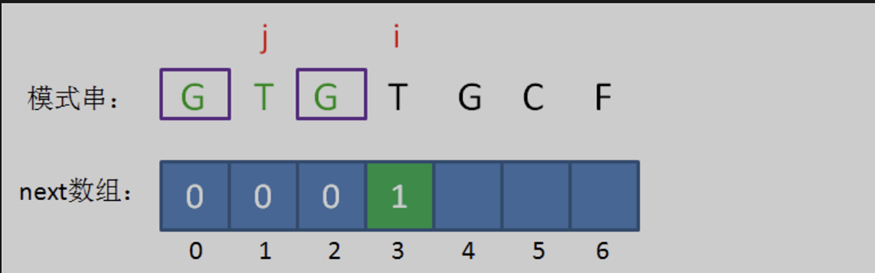
所以当i=3时,j=1,next[ 3 ] = next[ 2 ] + 1 = 1。
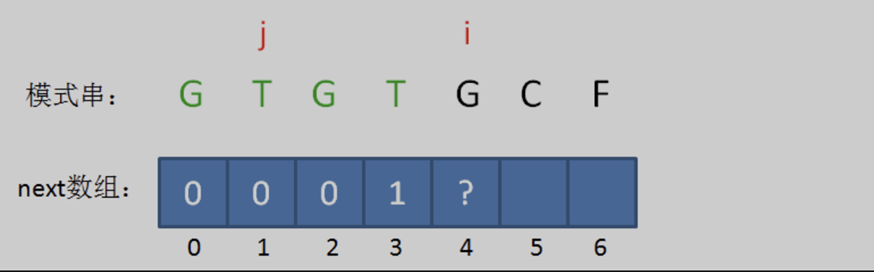
继续后移。此时的已匹配前缀是 “GTGT“,由于模式串中 pat [j] == pat [i-1],即 ‘T’ = ‘T’,最长可匹配前缀子串又增加了一位,是 ”GT“。
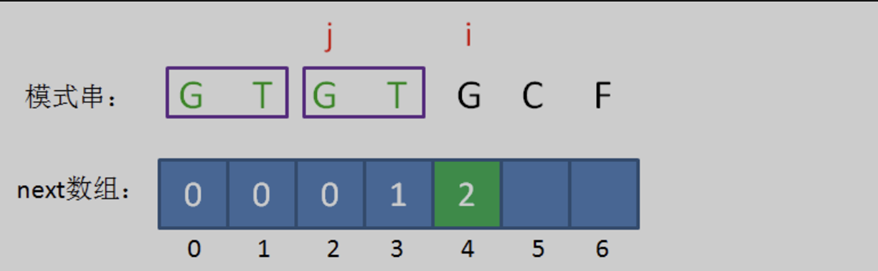
所以当i=4时,j=2,next[ 4 ] = next[ 3 ] + 1 = 2。
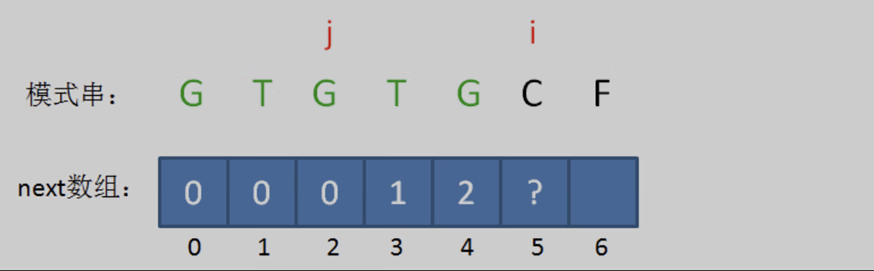
此时的已匹配前缀是 “GTGTG“,由于模式串当中 pat [ j ] == pat [ i-1 ],即 ‘G’ = ‘G’,最长可匹配前缀子串又增加了一位,是 ”GTG“。
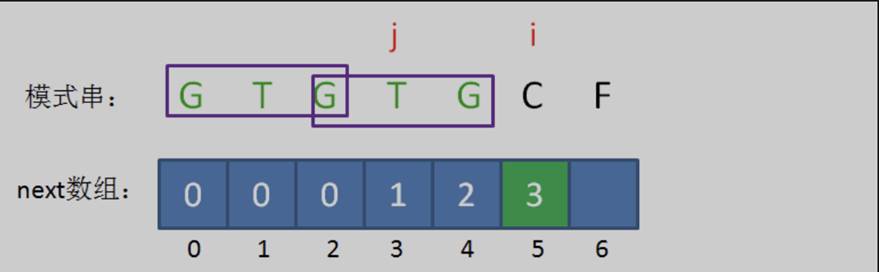
所以当i=5时,j=3,next[ 5 ] = next[ 4 ] + 1 = 3。
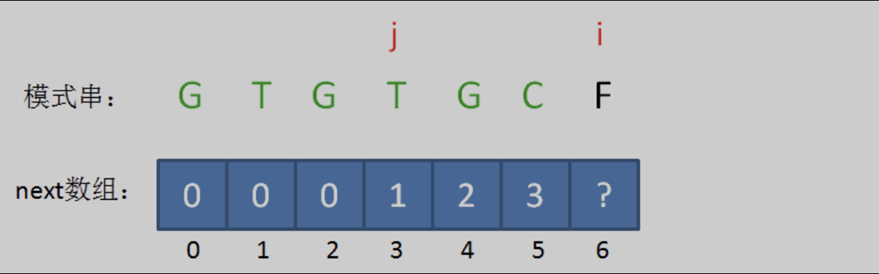
此时的已匹配前缀是 “GTGTGC“。此时,模式串中 pat [ j ] != pat [ i-1 ],即 ‘T’ != ‘C’。此时无法从next[ 5 ]的值推导出next[ 6 ],而字符 ‘C’ 的前面又有两段重复的子串“GTG”。
【重难点】
我们要找的是最长公共前后缀子串,在之前的判断中,我们已经获得了两组满足条件的公共字串 “GT“ 与 ”GTG“。既然在当前 ”GTG “ 找不到满足的前缀,那就到上一个前缀 “GT” 去找。
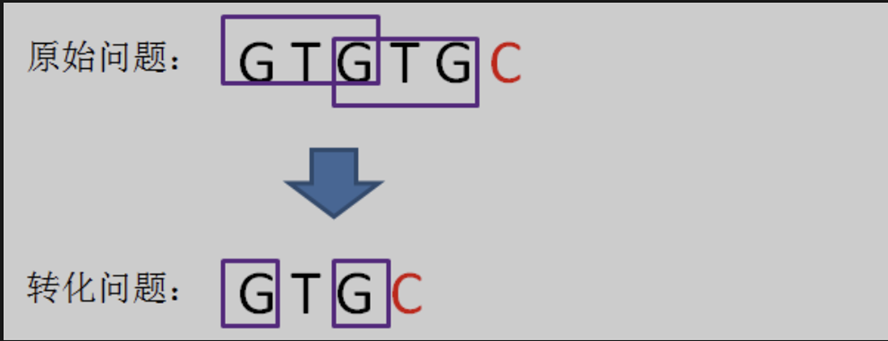
相当于把变量j回溯到了next[ j ],也就是j = 1的局面,在之前的前缀中寻找满足的前后缀子串。
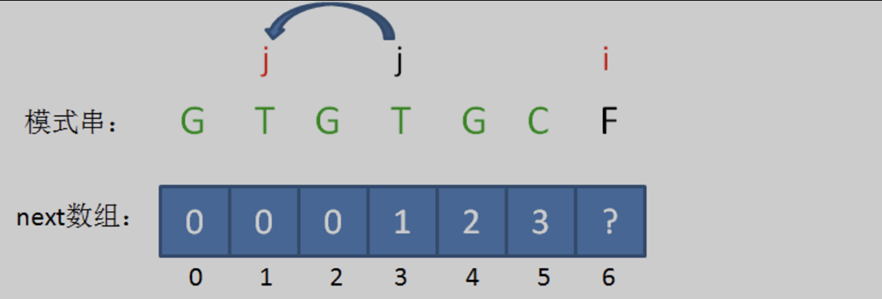
回溯后,情况仍然是 pat [ j ] != pat[ i-1 ],即 ’T’ != ‘C’。那就继续回溯。
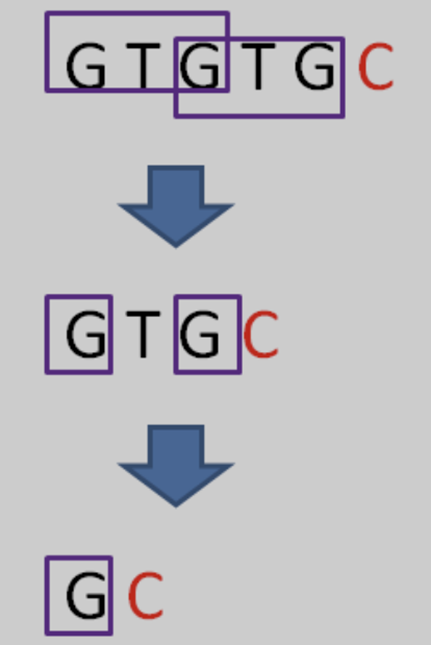
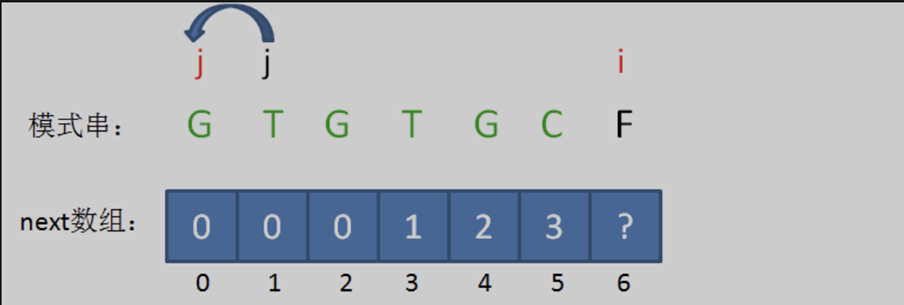
相当于再一次把变量 j 退回到了next[ j ],也就是 j = 0 的局面。
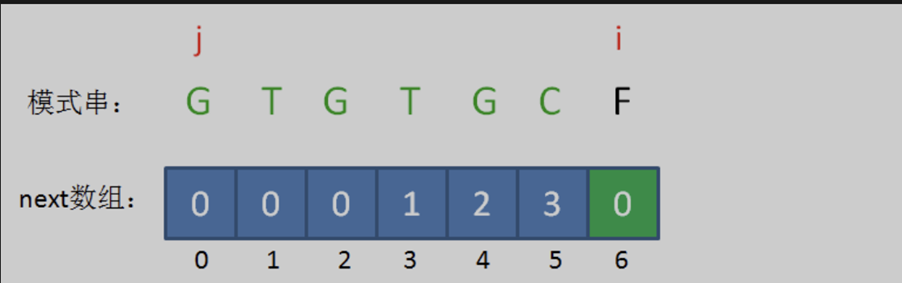
情况仍然是 pat [ j ] != pat[ i-1 ],即 ‘G’ != ‘C’。j 已经不能再回溯了,所以得出结论:i=6时,j=0,next[ 6 ] = 0。
小结:
1. 对模式串预处理,生成next数组
1.1 从next[ 2 ]开始,利用动态规划 + 双指针推推出跳转数组。
2. 进入主循环,遍历主串
2.1. 比较主串和模式串的字符。
2.2. 如果发现坏字符,查询next数组,得到匹配前缀所对应的最长可匹配前缀子串,移动模式串到对应位置。
2.3.如果当前字符匹配,继续循环。
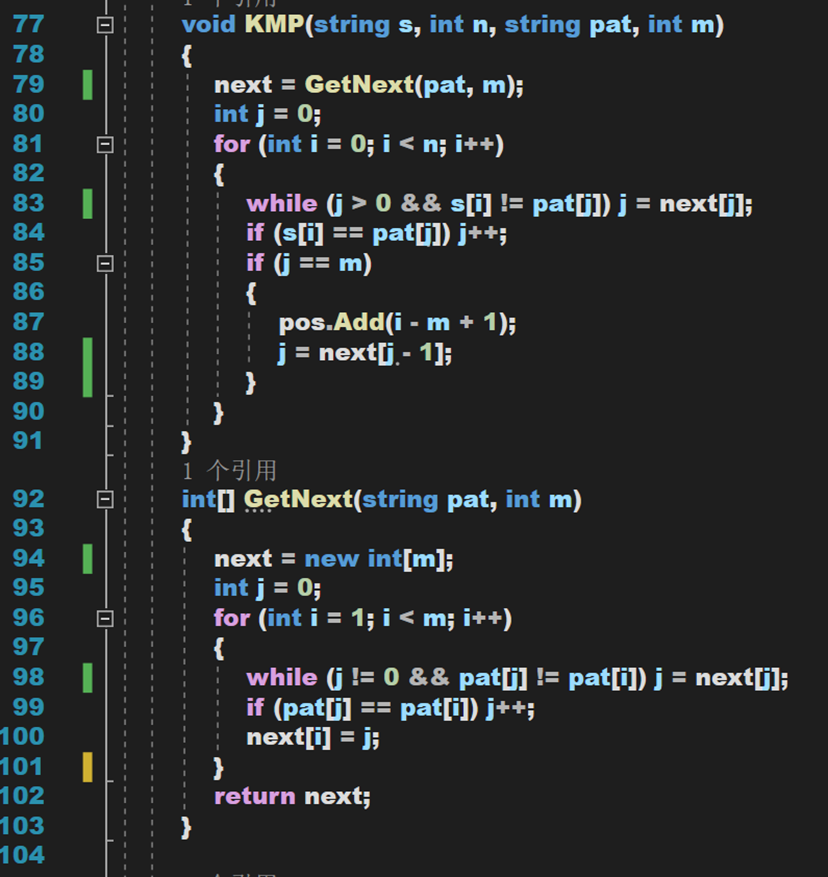
【注:有关 Line 88 行的分析,仅为个人推断,可能错在错误或解释不清的地方,望各位有想法的大佬及学者留言评论,谢谢!】
- Line 88:为什么要加这一句呢?如果是找第一次匹配的位置,那直接 return 结果就好。但是,我们需要找到模式串在主串中所有出现过的位置。这就使得我们需要保证,在找到一次匹配后,需要滑动到某一特定位置,再次开始匹配,且滑动后的位置需要保证不会漏掉任何一种情况。
据之前的分析,j = next[ j ] 表示将 j 回溯到上一个满足的前缀子串的下一次比较位置; j 表示的是当前应滑动到的比较位置。同理 j = next[ j – 1 ] 的含义肯定也是回溯到某一位置上。那为什么是 j – 1 呢?这里个人推断应该有如下两个方面:
(1)越界问题。进入到这个 if 内部的前提是 j == m,而 next 数组的最大索引位 m – 1。因此,为了防止越界,传入 next 中的值应当在 [0, m – 1] 之内。
(2)合理转化。
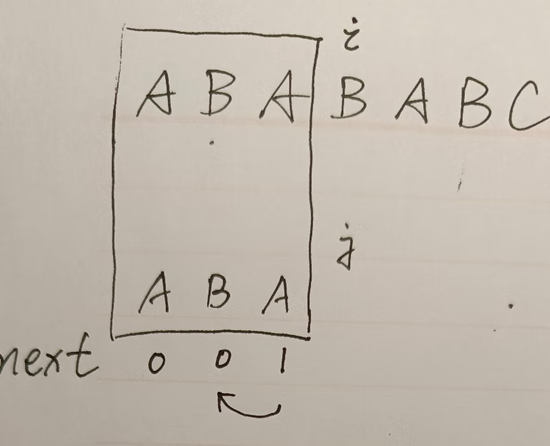
这是当前的状态,我们可以将当前 j 的位置补一个空白字符,其不与任何一个字符相匹配,因此需要回溯。那么对于当前前缀子串 “ABA#” 其不存在对应的可匹配前后缀子串,根据上面的规则,需要在之前找到一组可匹配的前后缀子串,重新进行判断。而如何滑动到之前的可匹配子串呢?我们可以把 j 的前一位视作当前的比较位置,假设该位置的字符是不匹配的,这样就可以直接回溯到之前的可匹配子串的下一次比较位置。因此,此处位 j = next[ j – 1 ]。
复杂度分析:
现在,该算法第一次计算t的哈希值时,时间复杂度为O(n);后续计算哈希值因为利用了滑窗的优化只有O(1);比较字符串的Equals()方法,一般地,可以视为O(1)。
- 总时间复杂度为O( m + n ),其中计算 next 数组的时间为 O( m );匹配时 时间为 O( n )。
- 空间复杂度为O( m ),使用了一个 next 数组,其中 m 为模式串的长度。
照例,测一下刚才的题
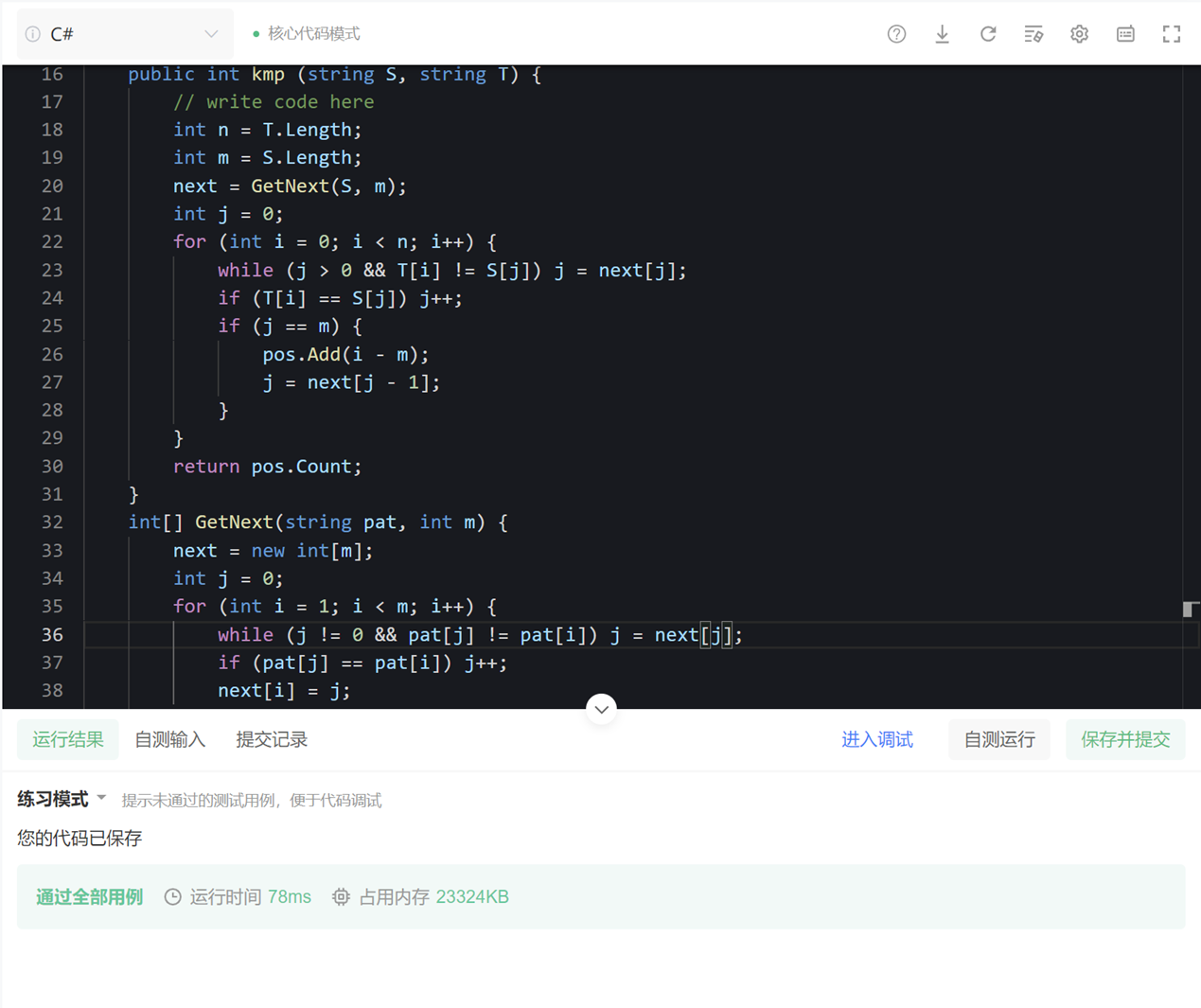
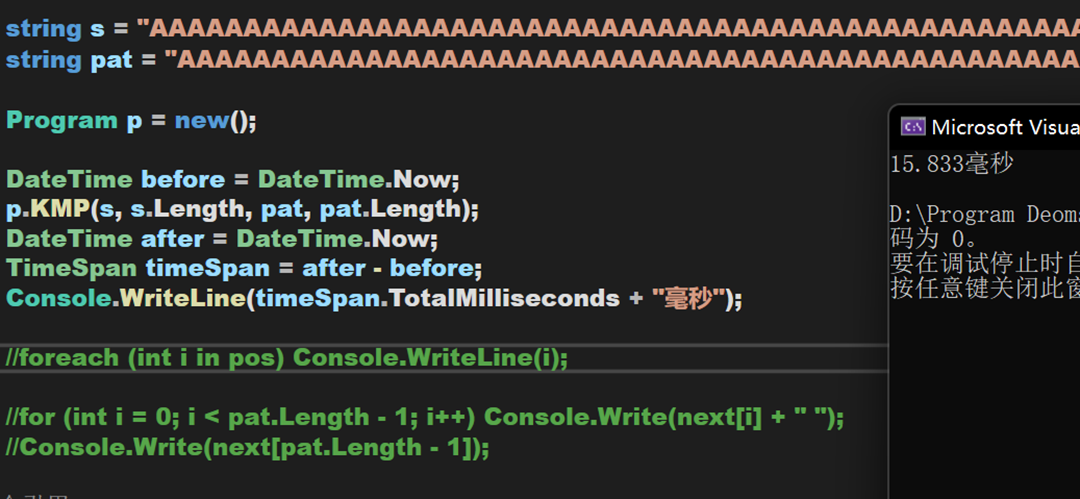
可以发现,即使面对很高数量级的数据,其效率是RK算法的两倍。
【注意:用此代码提交洛谷的题目(P3375 【模板】KMP字符串匹配 - 洛谷)会存在两个点超时,另一位使用C#提交的Coder也发生了同样的问题。推测可能是运行环境的原因,洛谷上的C#运行环境为C# MONO,其优化与相关底层逻辑并不如现行的 .NET 。力扣和牛客使用的运行环境分别是 .NET 6/C# 10 与 mcs5.4 ,因此一般不会出现卡语言的情况】

4. BM算法(Boyer-Moore)
【参考文章:字符串匹配算法:KMP与BM - AD_milk - 博客园 (cnblogs.com) 参考书籍:《数据结构与算法之美》】
虽然KMP比较出名,但在效率上有很多的算法都比它要好,如BM算法,其效率要比KMP好上3到4倍。当模式串长度较短时,二者效率基本相近;随着模式串 pat 的长度增大,BM的优势也逐渐凸显出来。原因可能在于,BM属于贪心算法,适应于实际应用,同时,贪心也是思考问题最直接的方式;KMP是稳定算法,中规中矩,按规矩办事,不在乎特例。
首先抛出两个定义:
(1)坏字符规则:指待匹配串和主串当中不匹配的字符,将主串的的该字符定义为坏字符。
BM算法与我们平常接触的字符串比较方法不同,它是按模式串从大到小的顺序,倒着比的。这样做也是有好处的,起码直观上是这样感觉的,贪心也是凭感觉嘛。就像做选择题,出卷老师为了让你花的时间久一点,故意把正确答案放到C跟D上。所以根据统计规律聪明点的做法应该是先算C跟D。
举个例子:

从模式串的末尾开始比较,当前主串的字符 ‘C’ 与模式串的字符 ’D’,将其定义为“坏字符”,有该字符存在,则无论之前匹不匹配,模式串均不可能在包含该坏字符的字串内被匹配。

俗话说:“三十六计走为上计“,既然你不满足我那我就开溜,直接向后移动6位,从没有坏字符的地方开始匹配。配着配着,发现又不满足了,定义坏字符为 ‘T‘ ,所以继续后移。
据此我们可以发现一个规律:当不匹配时,设坏字符对应的模式串中的字符,在模式串中的下标为 si (相对下标)。若坏字符在模式串中存在,则把这个坏字符在模式串中的下标记为 xi;不存在,则把 xi 记为 -1。且这样的坏字符在模式串中若存在多个,则总是选择最靠后的一个下标,以此保证不会因滑动过多而略过某些情况。那么,模式串向后滑动的位数 k = si – xi。图解参阅如下:

(2) 好后缀规则:指待匹配串和主串当中相匹配的后缀。
利用坏字符规则,BM在最优情况下的时间复杂度为 O( n / m ),例如主串为 aaabaaabaaabaaab,模式串为 aaaa,每次均可向后滑动四位。但只有这一个规则还不够,因为 k 可能为负数,如主串为 aaaaaaaaaaaa,模式串为 baaa。因此,我们又引入一个规则:好后缀规则。
依旧来举例说明:

将已经匹配的 “BC” 称为好后缀,记作 { u }。我们用它在模式串中寻找另一个与好后缀匹配的字符串 { u* }。

如果存在,则将模式串滑动到子串 { u* } 与好后缀 { u } 上下对齐的位置。

如果不存在,则直接滑动到好后缀 { u } 的后面。

此外,若在模式串中若存在多个与好后缀匹配的相同字符串或与好后缀的后缀字串相同的模式串中的前缀子串,则选择最长且靠后的串并记为 { v },按规则滑动。
以上就是BM算法的两个核心规则,在使用中可以分别计算好使用两用规则的滑动位数,取较大的一个 max( k1, k2 ),作为向后滑动的位数,这样既能使得时间复杂度接近最优的O( n / m ),也能避免滑动位数出现负数的情况。
具体实现如下:
(1)对于坏字符规则的计算,如果每次都去遍历那效率会很低,可以利用一个哈希表,存储每个字符在模式串中的位置,如果有多个相同字符,则取下标最大的一个。如图:
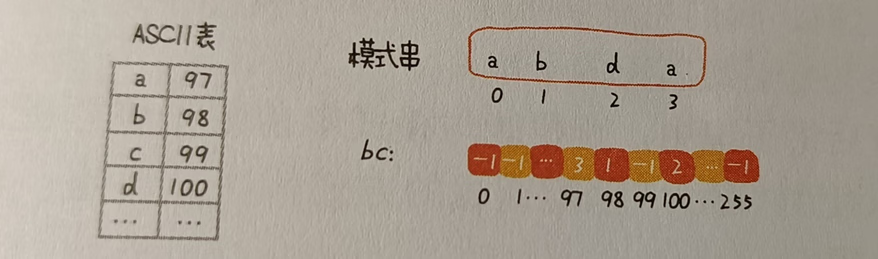

(2)对于好后缀规则,其核心在于:在模式串中查找与好后缀匹配的子串;在好后缀的所有后缀字串中,查找能与模式串前缀子串匹配的最长子串。
- 先来解决第一个问题,如何表示模式串中不同的后缀字串以及如何滑动到对应位置?
分析可知,后缀子串的最后一个字符的位置是固定且唯一的,因此只需通过后缀子串的长度即可进行唯一标识。然后引入一个数组suffix,数组下标表示后缀子串的长度(下标唯一且不变,子串最后一个字符的位置唯一且不变),对应数组值表示与其匹配的另一个子串的起始下标。如图:

如果存在多个合法的子串,则取下标最大的一个。
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 找完了模式串中的所有子串,还有一个问题:查找在好后缀的所有后缀子串中,能与模式串前缀子串匹配的最长的一个后缀子串(以下记为 “最长可匹配后缀子串”)
同样,为了避免每次遍历带来的时间消耗问题,我们对其也进行预处理。因为已经用数组 suffix 记录了滑动的规则,因此现在只需记录是否需要滑动即可。定义一个bool类型的数组 prefix,记录模式串的每个后缀子串是否能匹配模式串的前缀子串。如图:

—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 接下来,理解并推导一下这两个数组的值
用模式串的前缀子串,即下标为 [ 0, i ] ( 0 <= i <= m – 2 )的子串,与整个模式串求公共后缀子串。若公共后缀字串的长度为 k ,在前缀子串中的起始下标为 j ,则记录 suffix[ k ] = j 。若 j = 0,说明公共后缀子串是模式串的前子串,那就记录prefix[ k ] = true。相当于将字符串分为两部分,若存在两部分完全相同,则记录为 true。

—— —— —— —— —— —— —— —— —— —— —— —— —— ——
- 最后来看一下,如何根据这两个数组计算出滑动的位数
设好后缀长度为 k,用好后缀 { u } 在数组 suffix 中查找可匹配子串。若 suffix[ k ] ≠ -1,说明存在可匹配字串,则将模式串往后移动 j – suffix[ k ] + 1 位,其中 j 表示坏字符对应模式串中的下标位置。如图:
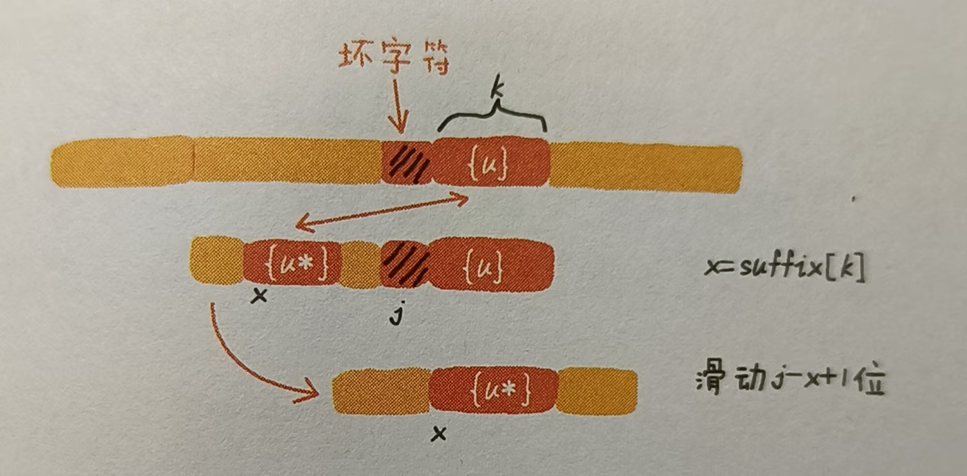
如果 suffix[ k ] = -1,说明模式串中不存在与好后缀匹配的子串。此时,使用好后缀的另一条规则:查找好后缀中,所有后缀子串中,能与模式串前缀子串匹配的,最长的那一个后缀子串。好后缀 pat[ j + 1, m – 1 ]的后缀子串 pat[ r, m – 1]( j + 2 <= r <= m – 1 )记作 { v },其长度 k = m – r。若 prefix[ k ] = true,表示长度为 k 的后缀子串,存在可匹配的前缀子串 { v* },则将模式串移动 r 位。如图:
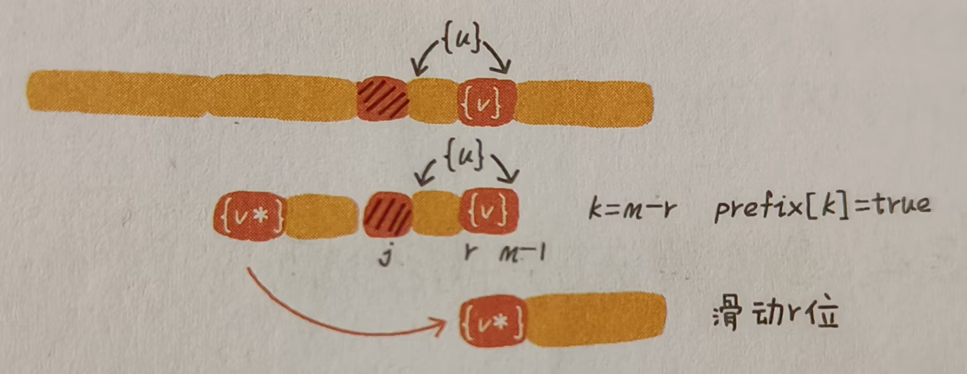
如果在模式串中没有找到与好后缀可以匹配的前缀子串,也没有找到好后缀中可匹配模式串中前缀子串的,后缀子串,则将整个模式串后移 m 位。如图:
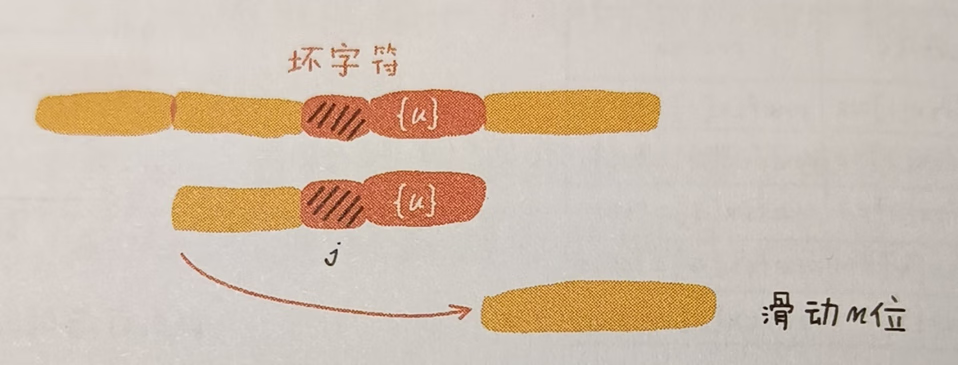
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
代码实现:【注:考虑到时间成本与篇幅问题,在此不做BM算法的同意主串多次匹配问题,如有兴趣欢迎自行研究,本人也可能会在今后放出可对同一主串多次匹配的代码】
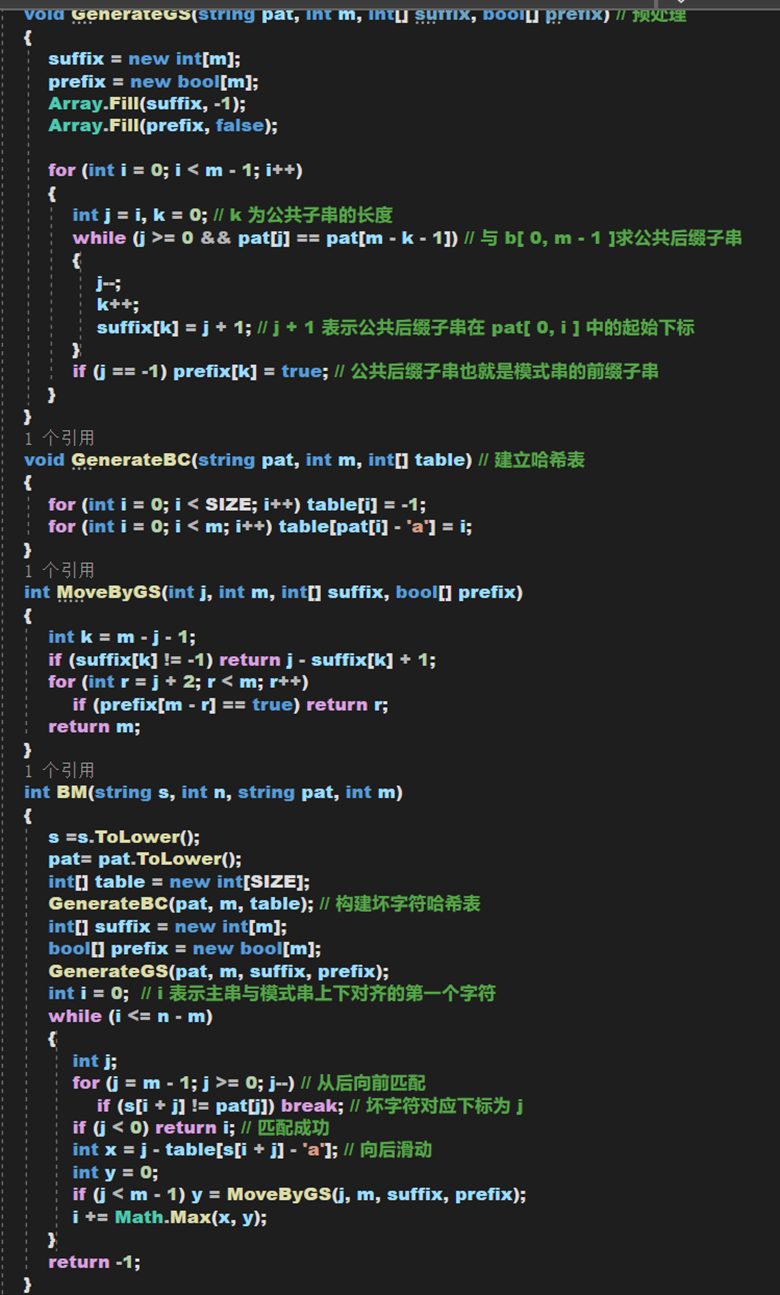
复杂度分析:
- 时间复杂度为O( n ) 若模式串中包含大量重复字符,则计算两个数组的时间将会达到 O( m2 ),但一般不会出现这样的极端情况。
- 空间复杂度为O( m )
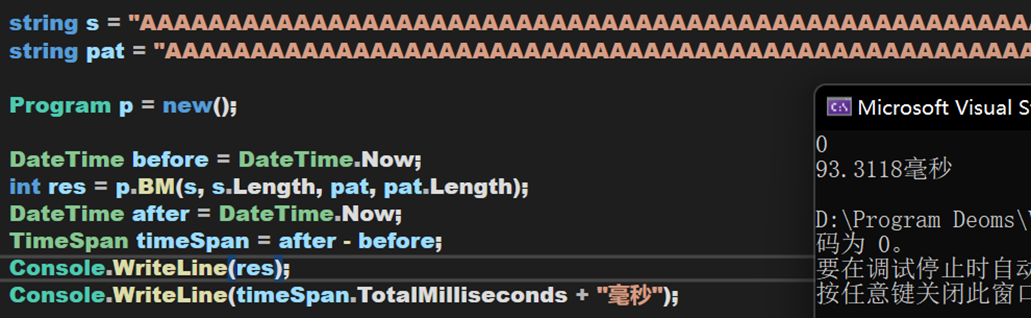
这就是一种极端情况,存在大量重复字符,导致其效率严重下降。
总结
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
至此,四种匹配方法全部介绍完毕,总结一下:
1. BF纯暴力算法,一位以为比较,遇到不匹配的从模式串开头在此一位一位比较。时间复杂度较高,但简洁明了思路清晰,因此在实际应用中最为常用。
2. RK算法,基于BF的比较字符的思想,转化为比较子串的哈希值。数值间的比较确实比字符比较快,而且利用滑窗的思想将计算哈希的时间复杂度将为 O( n ),但容易存在哈希冲突的问题,冲突后需要对 两部分子串进行完整比较。计算哈希方式越简单、字符串越长,冲突的概率越高,复杂度也会接近 O( n2 )。
3. KMP算法,利用某一特殊的规律,减少在不匹配时向后退回的位数,以达到降低时间复杂度的目的。
4. BM算法,结合贪心思想,进一步对KMP进行优化。但这两种方法过于复杂,掌握很不容易。
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
—— —— —— —— —— —— —— —— —— —— —— —— —— ——
[附 BF算法代码]
void BF(string s, int n, string pat, int m)
{
for (int i = 0; i <= n - m; i++)
{
int j = 0;
while (j < m)
{
if (s[i + j] != pat[j]) break;
j++;
}
if (j == m) pos.Add(i);
}
}
[附 RK算法代码]
void RK(string s, int n, string pat, int m)
{
int patCode = GetHash(pat);
int sCode = GetHash(s.Substring(0, m));
for (int i = 0; i <= n - m; i++)
{
if (patCode == sCode && ComString(i, s, pat)) pos.Add(i);
if (i < n - m) sCode = NextHash(s, sCode, i, m);
}
}
int GetHash(string str)
{
int hash = 0, n = str.Length;
for (int i = 0; i < n; i++) hash += str[i] - 'a';
return hash;
}
int NextHash(string str, int hash, int idx, int len)
{
hash -= str[idx] - 'a';
hash += str[idx + len] - 'a';
return hash;
}
bool ComString(int idx, string s, string pat)
{
return pat == s.Substring(idx, pat.Length);
}
[附 KMP算法代码]
void KMP(string s, int n, string pat, int m)
{
next = GetNext(pat, m);
int j = 0;
for (int i = 0; i < n; i++)
{
while (j > 0 && s[i] != pat[j]) j = next[j];
if (s[i] == pat[j]) j++;
if (j == m)
{
pos.Add(i - m + 1);
j = next[j - 1];
}
}
}
int[] GetNext(string pat, int m)
{
next = new int[m];
int j = 0;
for (int i = 1; i < m; i++)
{
while (j != 0 && pat[j] != pat[i]) j = next[j];
if (pat[j] == pat[i]) j++;
next[i] = j;
}
foreach (int i in next) Console.Write(i + " ");
return next;
}
[附 BM算法代码]
static int SIZE = 26;
void GenerateGS(string pat, int m, int[] suffix, bool[] prefix) // 预处理
{
suffix = new int[m];
prefix = new bool[m];
Array.Fill(suffix, -1);
Array.Fill(prefix, false);
for (int i = 0; i < m - 1; i++)
{
int j = i, k = 0; // k 为公共子串的长度
while (j >= 0 && pat[j] == pat[m - k - 1]) // 与 b[ 0, m - 1 ]求公共后缀子串
{
j--;
k++;
suffix[k] = j + 1; // j + 1 表示公共后缀子串在 pat[ 0, i ] 中的起始下标
}
if (j == -1) prefix[k] = true; // 公共后缀子串也就是模式串的前缀子串
}
}
void GenerateBC(string pat, int m, int[] table) // 建立哈希表
{
for (int i = 0; i < SIZE; i++) table[i] = -1;
for (int i = 0; i < m; i++) table[pat[i] - 'a'] = i;
}
int MoveByGS(int j, int m, int[] suffix, bool[] prefix)
{
int k = m - j - 1;
if (suffix[k] != -1) return j - suffix[k] + 1;
for (int r = j + 2; r < m; r++)
if (prefix[m - r] == true) return r;
return m;
}
int BM(string s, int n, string pat, int m)
{
s = s.ToLower();
pat = pat.ToLower();
int[] table = new int[SIZE];
GenerateBC(pat, m, table); // 构建坏字符哈希表
int[] suffix = new int[m];
bool[] prefix = new bool[m];
GenerateGS(pat, m, suffix, prefix);
int i = 0; // i 表示主串与模式串上下对齐的第一个字符
while (i <= n - m)
{
int j;
for (j = m - 1; j >= 0; j--) // 从后向前匹配
if (s[i + j] != pat[j]) break; // 坏字符对应下标为 j
if (j < 0) return i; // 匹配成功
int x = j - table[s[i + j] - 'a']; // 向后滑动
int y = 0;
if (j < m - 1) y = MoveByGS(j, m, suffix, prefix);
i += Math.Max(x, y);
}
return -1;
}
[# 有关Intrinsic、Attribute与“内在属性”]
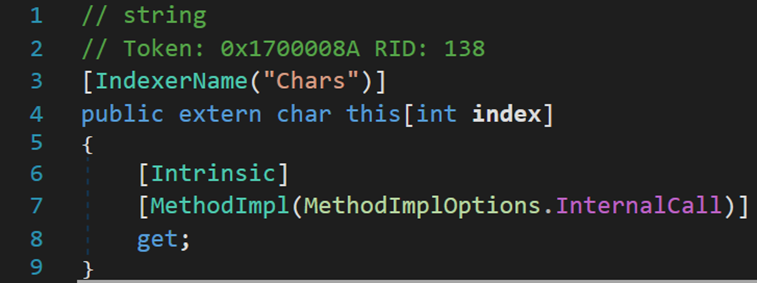
[Intrinsic] 被称为内在属性,我们把形如 [xxxx] 的表达式称为内在属性,如 [Serializable]、[IndexerName("Chars")]、[MethodImpl(MethodImplOptions.InternalCall)]等。

通过追踪发现其派生于类Attribute。在分析该内在属性前,先来看看什么是 Attribute。
1. 类 Attritube
这里要注意,属性和特性的区别。在微软翻译器上,Arrtibute 被翻译为属性,这个翻译在 C# 中并不准确。
- 属性:又叫智能字段,是类的成员,是面向对象编程语言的一个基本概念,提供了安全和灵活的数据访问封装,不存储数据。
- 特性:特性本质上是一个类,用来为目标元素提供附加信息,并在运行时通过反射机制来获取这些信息以影响或控制应用程序运行时的行为。目标元素可以是程序集、类、构造函数、委托、枚举、事件、字段、接口、方法、可移植可执行文件模块、参数、属性、返回值、结构或其他特性。
限于篇幅,在此就简单描述一下这个类的基本信息与功能。一般地,我们并不直接使用这个类,而是较多的使用其派生出的类
此处仅展示部分,派生的类有很多,每个类之下有不同的内容,其内容用于规定被修饰的对象应当怎样做或只能怎样做。如:AttributeUsage(AttributeTargets.Method) 。其中,AttributeTargets 用于指定对哪些程序元素使用;而 AttributeTargets.Method 表示被修饰的对象只能被方法体使用。
在 .NET 中,提供了三种预定义的特性:AttributeUsage、Conditional 与 Obsolete。
- AttributeUsage:描述了如何使用一个自定义特性类。
- Conditional:标记了一个条件方法,其执行依赖于指定的预处理标识符。它会引起方法调用的条件编译,取决于指定的值,比如 Debug 或 Trace。
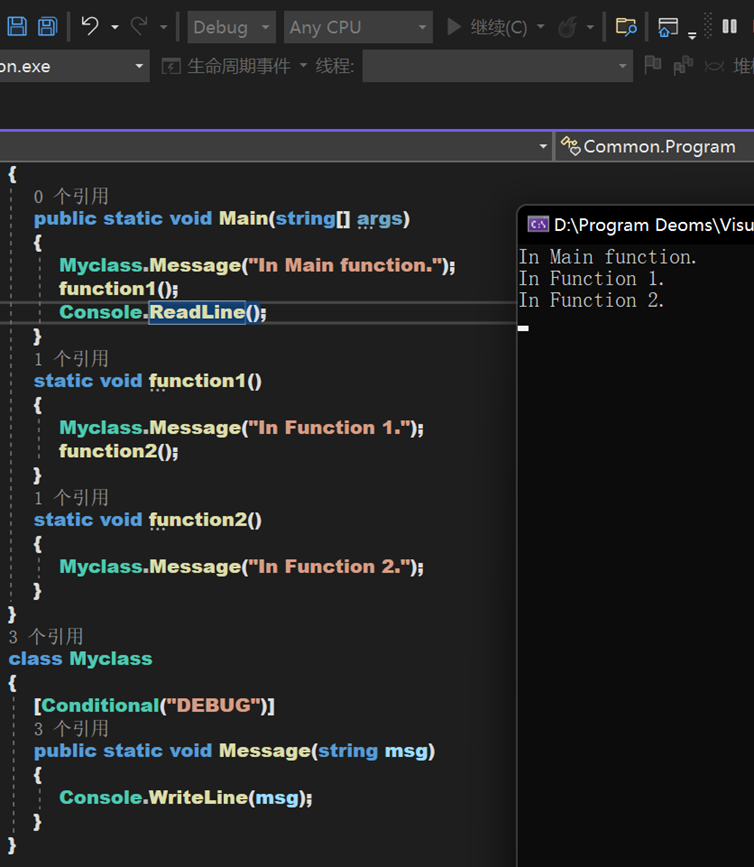
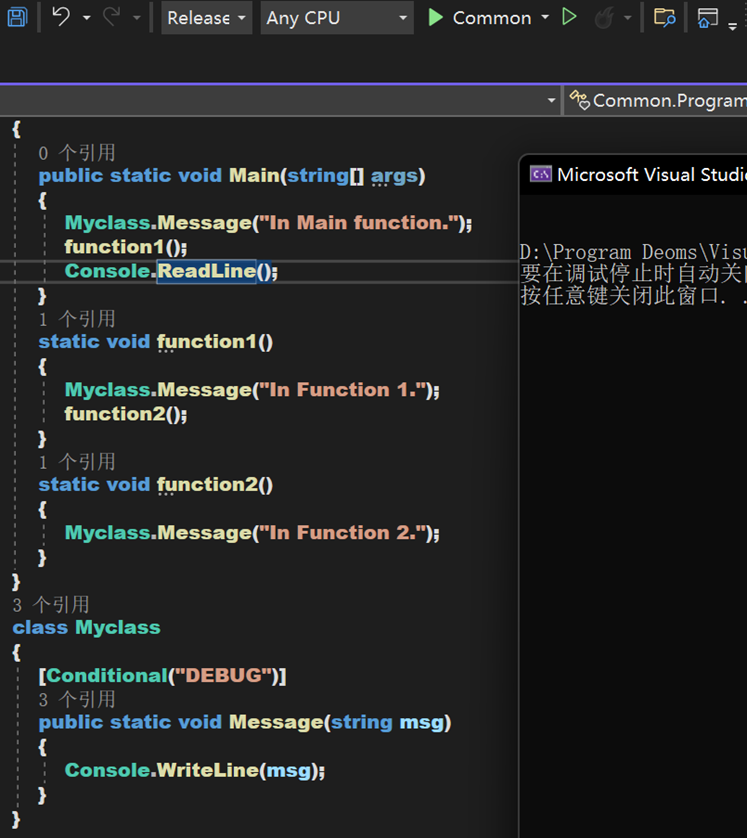
如,我们在方法上附加一个 Conditional 特性,使得其只在 DEGUB 模式下运行。
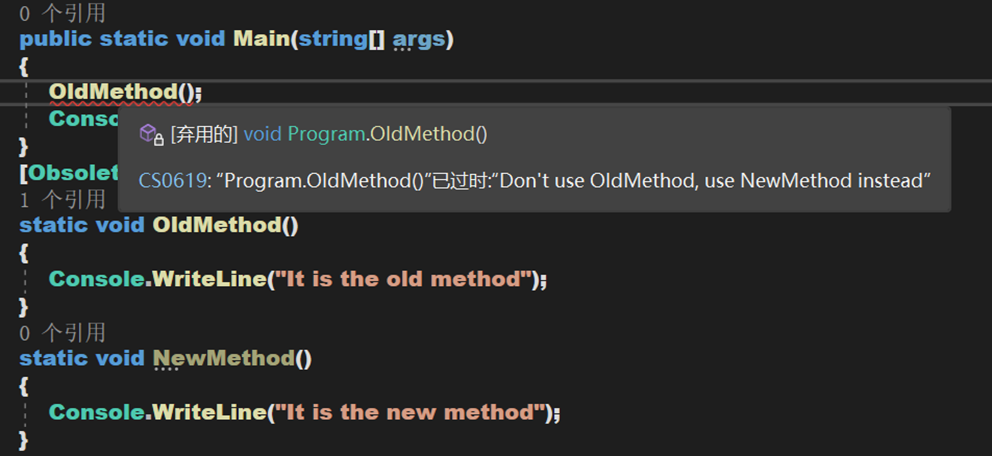
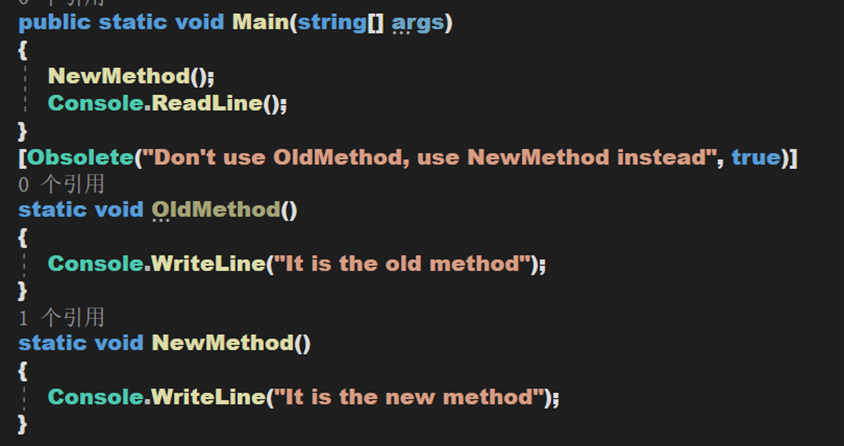
- Obsolete:用于标记不应被使用的程序实体。它可以让通知编译器丢弃某个特定的目标元素。如,当一个新方法被用在一个类中,但是仍然想要保留类中的旧方法,可以把它标记为 Obsolete(过时的)并输出输出信息。
2. 类 IntrinsicAttribute
关于特性 Intrinsic,在 dotnet/corefx 中找到其相关注释如下:

- Calls to methods or references to fields marked with this attribute may be replaced at ome call sites with jit intrinsic expansions. 微软翻译:某些调用站点中,对使用此属性标记的方法的调用或对使用此属性标记的字段的引用可能会替换为 JIT扩展。说人话就是,被该属性标记的方法或字段,可能会被 JIT 替换/优化成功能相同的方法或字段。
- Types marked with this attribute may be specially treated by the runtime/compiler. 微软翻译:运行时/编译器可能会专门处理使用此属性标记的类型。也就是说,被该内在属性标记的对象确实会进行专门的处理。
举个粗略的例子:JIT-optimizer 可以代替 Enum.HasFlag 在某些情况下进行简单的按位比较,而在其他情况下则不然。为此,它需要将方法标识为 Enum.HasFlag ,检查一些条件并将其替换为更优化的实现。虽然优化器可以通过名称识别方法,但出于性能原因,最好在执行字符串比较之前通过简单的标志过滤掉方法,即在编译阶段就将要优化的部分识别出来,而不是将其交给优化器来进行识别工作。
下面,简单解释一下其运行流程:

留言评论