P2216 [HAOI2007]理想的正方形方法记录

乎语百科 2022-10-11 20:25:10 281 0

[HAOI2007]理想的正方形

题目描述

有一个 \(a \times b\) 的整数组成的矩阵，现请你从中找出一个 \(n \times n\) 的正方形区域，使得该区域所有数中的最大值和最小值的差最小。

输入格式

第一行为 \(3\) 个整数，分别表示 \(a,b,n\) 的值。

第二行至第 \(a+1\) 行每行为 \(b\) 个非负整数，表示矩阵中相应位置上的数。每行相邻两数之间用一空格分隔。

输出格式

仅一个整数，为 \(a \times b\) 矩阵中所有“ \(n \times n\) 正方形区域中的最大整数和最小整数的差值”的最小值。

样例 #1

样例输入 #1

样例输出 #1

提示

问题规模。

矩阵中的所有数都不超过 \(1,000,000,000\)。

\(20\%\) 的数据 \(2 \le a,b \le 100,n \le a,n \le b,n \le 10\)。

\(100\%\) 的数据 \(2 \le a,b \le 1000,n \le a,n \le b,n \le 100\)。

题解

前置知识

试想一下，如果我们把\(a*b\)的矩阵改为长度为\(a\)的序列，要找的东西变成长度为\(n\)的子段，那不就变成单调队列之滑动窗口了嘛。

可以先看看我写的这篇关于滑动窗口的博客。

有了这些对单调队列的基本认知，我们不难想出一种本题的做法。

方法分析

首先可以将\(a*b\)的矩阵理解为\(b\)行长度为\(a\)的序列，然后对每一行的序列使用“滑动窗口”，这样就可以处理出每一行中长度为\(n\)的子段中所有数的最大值和最小值。

我们用\(board[i][j]\)来存原来的矩阵，用\(x1[i][j]\)和\(x2[i][j]\)分别记录第\(i\)行第\(j\)个窗口的最小值和最大值。那么我们每一行就能产生\(b-n+1\)个窗口。处理出来的\(x1\)和\(x2\)规模就是\(a*(b-n+1)\).

for(int i=1;i<=a;i++)
	{
		int h=0,t=0;
		memset(q1,0,sizeof(q1));
		memset(q2,0,sizeof(q2));
		for(int j=1;j<=b;j++)
		{
			while(h<=t&&j-q1[h]>=n) h++;
			while(h<=t&&board[i][j]<board[i][q1[t]]) t--;
			q1[++t]=j;
			if(j>=n) x1[i][j-n+1]=board[i][q1[h]];
		}
		for(int j=1;j<=b;j++)
		{
			while(h<=t&&j-q2[h]>=n) h++;
			while(h<=t&&board[i][j]>board[i][q2[t]]) t--;
			q2[++t]=j;
			if(j>=n) x2[i][j-n+1]=board[i][q2[h]];
		}
	}

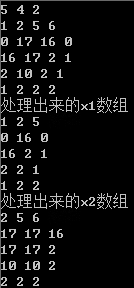
然后我们在处理好的\(x1\)和\(x2\)基础上，对每一列使用“滑动窗口”。如果说每一行的滑动窗口是从左往右滑动的，那么每一列的滑动窗口就是从上往下滑动的。

我们用用\(y1[i][j]\)和\(y2[i][j]\)分别记录第\(i\)列第\(j\)个窗口的最小值和最大值。那么我们每一列就能产生\(a-n+1\)个窗口。处理出来的\(y1\)和\(y2\)规模就是\((a-n+1)*(b-n+1)\).

for(int i=1;i<=b-n+1;i++)
	{
		int h=0,t=0;
		memset(q1,0,sizeof(q1));
		memset(q2,0,sizeof(q2));
		for(int j=1;j<=a;j++)
		{
			while(h<=t&&j-q1[h]>=n) h++;
			while(h<=t&&x1[j][i]<x1[q1[t]][i]) t--;
			q1[++t]=j;
			if(j>=n) y1[j-n+1][i]=x1[q1[h]][i];
		}
		for(int j=1;j<=a;j++)
		{
			while(h<=t&&j-q2[h]>=n) h++;
			while(h<=t&&x2[j][i]>x2[q2[t]][i]) t--;
			q2[++t]=j;
			if(j>=n) y2[j-n+1][i]=x2[q2[h]][i];
		}
	}

回想一下，\(x\)数组处理出的是每一行长度为\(n\)的子段中最小/最大值，\(y\)数组处理出的是\(x\)的基础上每一列长度为\(n\)的子段中最小/最大值，那么这样一来\(y\)数组中就是整个矩阵中\(n*n\)的正方形区域中的最小/最大值。

然后只需要遍历一遍，求出最小的\(y2[i][j]-y1[i][j]\)即可。

#include<iostream>
#include<cstring>
#include<cstdio>
#include<algorithm>
using namespace std;
const int N=1005;
int a,b,n;
int board[N][N];
int x1[N][N],x2[N][N],y1[N][N],y2[N][N];
int q1[N],q2[N];
int cntx1,cntx2,cnty1,cnty2;
int minn(int a,int b)
{
	return a<b?a:b;
}
int ans=2147483647;
int main()
{
	scanf("%d%d%d",&a,&b,&n);
	for(int i=1;i<=a;i++)
		for(int j=1;j<=b;j++)
			scanf("%d",&board[i][j]);
	for(int i=1;i<=a;i++)
	{
		int h=0,t=0;
		memset(q1,0,sizeof(q1));
		memset(q2,0,sizeof(q2));
		for(int j=1;j<=b;j++)
		{
			while(h<=t&&j-q1[h]>=n) h++;
			while(h<=t&&board[i][j]<board[i][q1[t]]) t--;
			q1[++t]=j;
			if(j>=n) x1[i][j-n+1]=board[i][q1[h]];
		}
		for(int j=1;j<=b;j++)
		{
			while(h<=t&&j-q2[h]>=n) h++;
			while(h<=t&&board[i][j]>board[i][q2[t]]) t--;
			q2[++t]=j;
			if(j>=n) x2[i][j-n+1]=board[i][q2[h]];
		}
	}
	memset(q1,0,sizeof(q1));
	memset(q2,0,sizeof(q2));
	for(int i=1;i<=b-n+1;i++)
	{
		int h=0,t=0;
		memset(q1,0,sizeof(q1));
		memset(q2,0,sizeof(q2));
		for(int j=1;j<=a;j++)
		{
			while(h<=t&&j-q1[h]>=n) h++;
			while(h<=t&&x1[j][i]<x1[q1[t]][i]) t--;
			q1[++t]=j;
			if(j>=n) y1[j-n+1][i]=x1[q1[h]][i];
		}
		for(int j=1;j<=a;j++)
		{
			while(h<=t&&j-q2[h]>=n) h++;
			while(h<=t&&x2[j][i]>x2[q2[t]][i]) t--;
			q2[++t]=j;
			if(j>=n) y2[j-n+1][i]=x2[q2[h]][i];
		}
	}
	for(int i=1;i<=a-n+1;i++)
		for(int j=1;j<=b-n+1;j++)
			ans=minn(ans,y2[i][j]-y1[i][j]);
	printf("%d\n",ans);
	return 0;
}

标签：

P2216 [HAOI2007]理想的正方形 方法记录