这一章我们来唠唠如何优化BERT对文本长度的限制。BERT使用的Transformer结构核心在于注意力机制强大的交互和记忆能力。不过Attention本身O(n^2)的计算和内存复杂度，也限制了Transformer在长文本中的应用。

之前对长文档的一些处理方案多是暴力截断，或者分段得到文本表征后再进行融合。这一章我们看下如何通过优化attention的计算方式，降低内存/计算复杂度，实现长文本建模。Google出品的Efficient Transformers: A Survey里面对更高效的Transformer魔改进行了分类，这一章我们主要介绍以下5个方向：

1. 以Transformer-XL为首的片段递归

2. Longformer等通过稀疏注意力，降低内存使用方案

3. Performer等通过矩阵分解，降低attention内积计算复杂度的低秩方案

4. Reformer等可学习pattern的注意力方案

5. Bigbird等固定pattern注意力机制

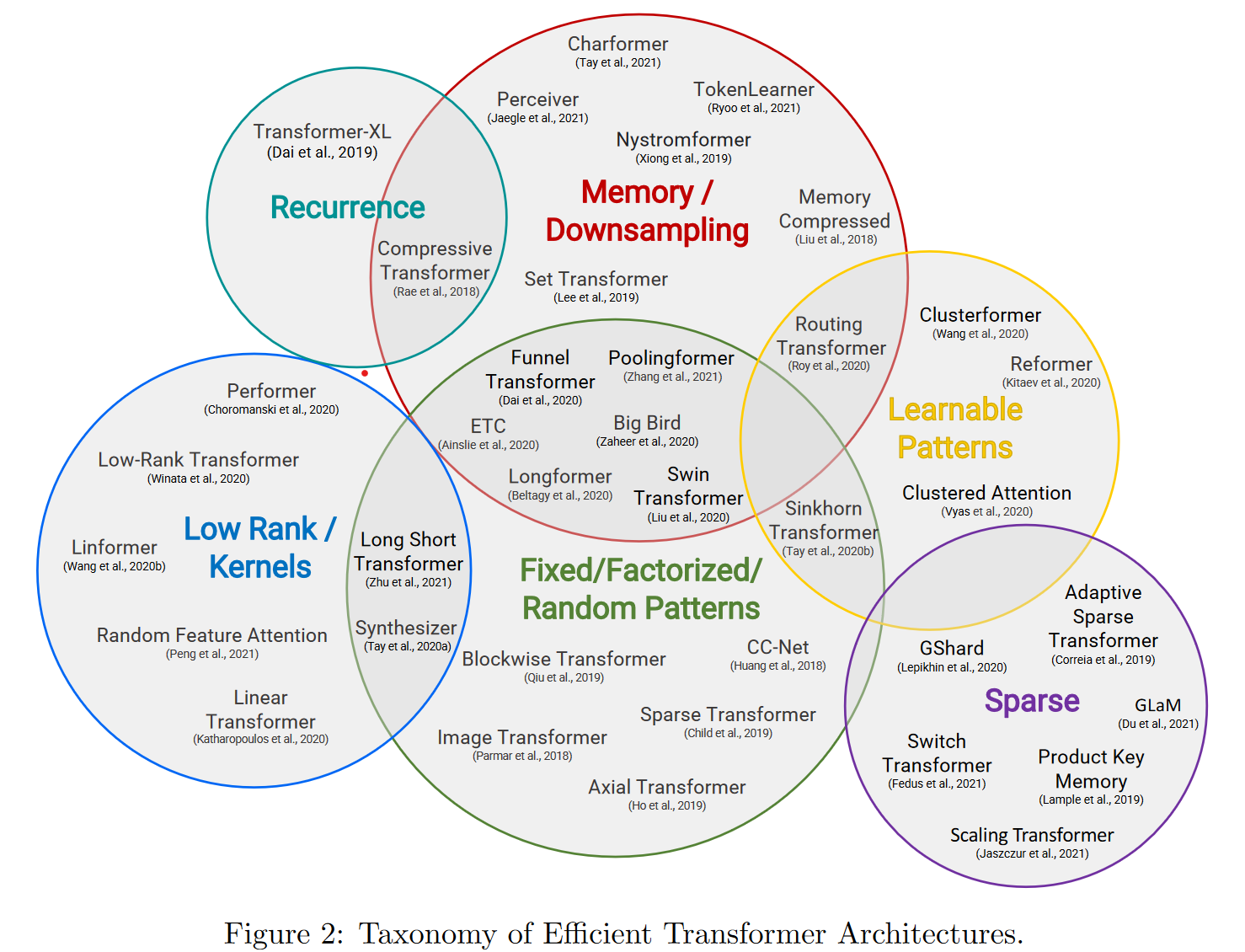
Transformer-xl

• paper: Transformer-XL: Attentive Language Models Beyond a Fixed-Length Context

• github：https://github.com/kimiyoung/transformer-xl

• Take Away: 相对位置编码 + 片段递归机制

为了突破Transformer对固定长度建模的限制，Transformer-xl提出了相对位置编码和片段递归的方案，后续也被XLNET沿用~

1. 片段递归

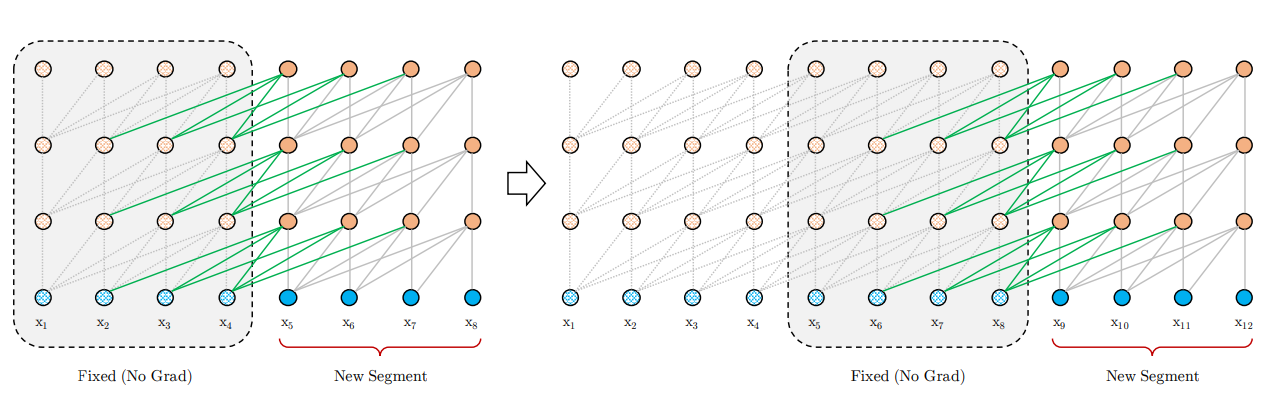
片段递归的思路其实很早就有，不过之前的方案多是保留上一个片段的last hidden state，作为当前片段的补充信息。而Transformer-xl则是直接保留并cache了上个片段的所有hidden state，和当前片段进行拼接，梯度更新时只更新当前片段的隐藏层。

具体的Attentenion计算中如下，\(\tau\)是片段，\(n\)是hidden layer，\(\circ\)是向量拼接，\(SG()\)是不进行梯度更新的意思。于是当前片段Q，K，V是由上个片段的隐藏层和当前片段的隐藏层拼接得到。每个片段完成计算后会把隐藏层计算结果进行存储，用于下个片段的计算，用空间换时间，既避免了重复计算，又使得新的片段能保留大部分的历史片段信息。这里的历史片段信息并不一定只使用T-1，理论上在内存允许的情况下可以拼接更多历史片段~

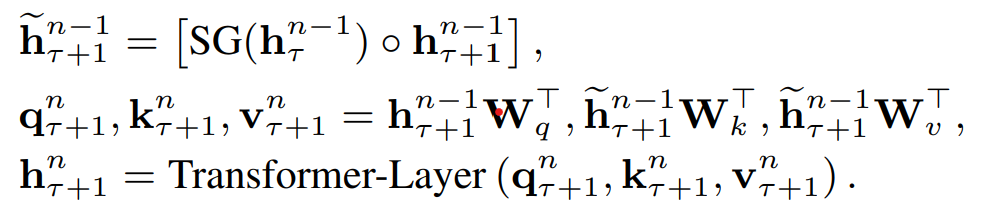
1. 相对位置编码

片段递归如果和绝对位置编码一起使用会存在问题，因为不同片段相同位置的 绝对位置编码相同，模型无法区分它们来自不同的片段。因此作者提出了相对位置编码。之前在讨论绝对位置编码不适用于NER任务时有分析过相对位置编码>>中文NER的那些事儿5. Transformer相对位置编码&TENER代码实现，这里我们再回顾下~

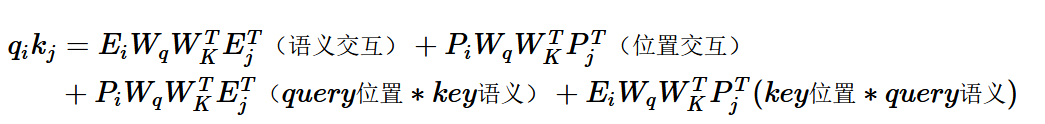
绝对位置编码是直接加到词向量上，在Attention计算中进行交互。把内积展开可以得到如上形式，包括4个部分：Query和Key的纯语义交互，各自的位置信息和语义的交互，以及反映相对距离的位置交互。

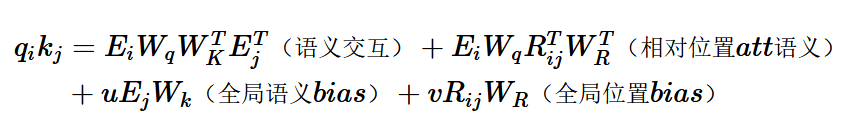
Transformer-XL的相对位置编码和以上的展开形式基本一一对应，也使用了三角函数的编码方式，只需要两点调整

• key对应的绝对位置编码\(p_j\)替换为两个token相对位置i-j的相对位置编码\(R_{i,j}\)

• query的位置编码\(P_iW_q\)替换成两个learnable的参数u和v

和以上绝对位置编码的Attention计算对比：

• 语义交互不变

• 位置交互：绝对位置编码内积替换为相对位置编码对应的全局位置偏置, 在表征距离的同时加入了方向信息

• query位置*key语义：因为交互是计算一个query token对全部key token的attention，所以这里的位置编码部分是个常量，作者替换为了trainable的参数u，于是这部分有了更明确的含义就是key对应的全局语义偏置

• query语义*key位置： 替换为query语义 * query和key的相对位置编码，也就是语义和位置交互

结合片段递归和相对位置编码，Transformer-xl突破了Transformer对固定文本长度的限制。同时片段递归和以下4种Transformer优化方案是正交的关系，可以在以下的四种方案中叠加使用片段递归去优化长文本建模

Longformer

• paper: Longformer: The Long-Document Transformer

• github：https://github.com/allenai/longformer

• 中文预训练模型：https://github.com/SCHENLIU/longformer-chinese

• Take Away: 滑动窗口稀疏注意力机制

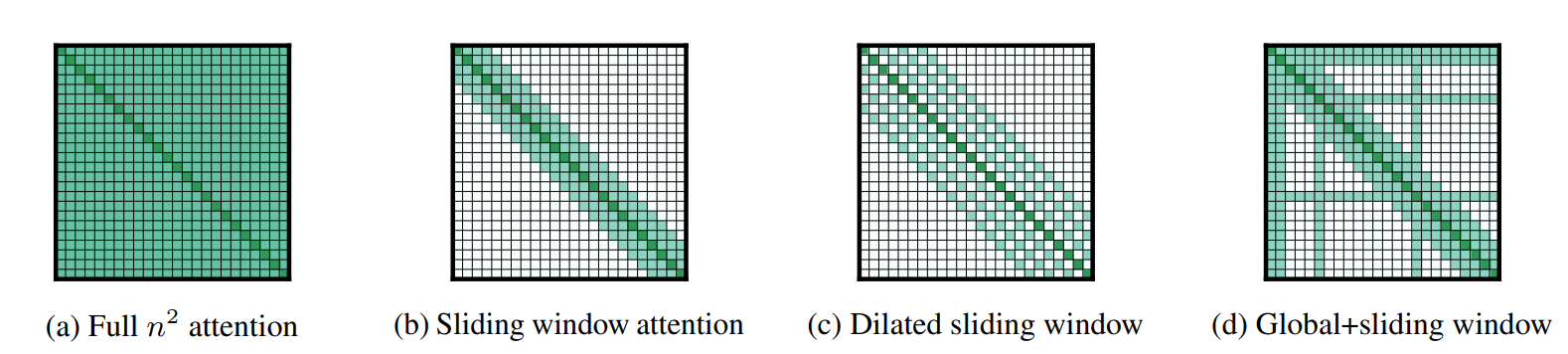
Longformer的3点主要创新是

1. 滑动窗口attention（图b）

解决attention计算复杂度最简单直观的方案，就是把原本all-2-all的attention计算限制到适当的window size(w)内，这样对于长度为n的序列，原本O(n^2)的复杂度就缩减到了O(n*w)。因为attention本质是引入当前token的上下文信息，但token其实很难和八丈远外的内容进行交互，所以合理的窗口选择并不会损失太多的信息，并且和stack-cnn相同更高的layer会拥有更大的感知野。Longformer这里选择了512作为窗口大小，attention的复杂度和BERT相同。

1. 空洞滑窗attention（图C）

和Dilated-CNN相同，这里作者也采用了dilation来扩大相同计算量下的感知野。不过感觉这里和CNN还是有些区别，图像使用Dilation因为单一像素本身信息有限，需要通过kernel来提取图片局部特征，而对文本序列来说，每个token就是最小粒度的信息元包含信息更多，因此dilation会带来更多的信息损失。不过作者在使用过程中也加了一些tricks，包括对多头的不同头使用不同的dilation策略，以及底层layer不使用dilation保留更多信息，更高层使用更大的dilation扩大感知野。不过在后面的消融实验中空洞滑窗的效果提升并不十分显著。

1. 任务导向全局attention（图d）

以上局部attenion在一些任务中存在不足，例如QA任务中可能问题无法和上下文进行完整交互，以及分类任务中CLS无法获得全部上下文信息。因此作者在下游任务微调中加入了针对部分token的全局attention。因此在下游微调时，需要进行全局交互的token，会用预训练的Q，K，V进行初始化，不过会用两套线性映射的参数分别对全局和滑动窗口的Q,K,V进行映射。

Longformer的预训练是在Roberta的基础上用长文本进行continue train。原始Roberta的position embedding只有512维，这里longformer把PE直接复制了8遍，得到4096维度的PE用于初始化，这样在有效保留原始PE局部信息的同时，也和以上512的window-size有了对应。至于longformer的效果，可以直接看和下面BigBird的对比。

Bigbird

• paper: Big Bird：Transformers for Longer Sequences

• github: https://github.com/google-research/bigbird

• Take Away: 使用补充固定token计算全局注意力

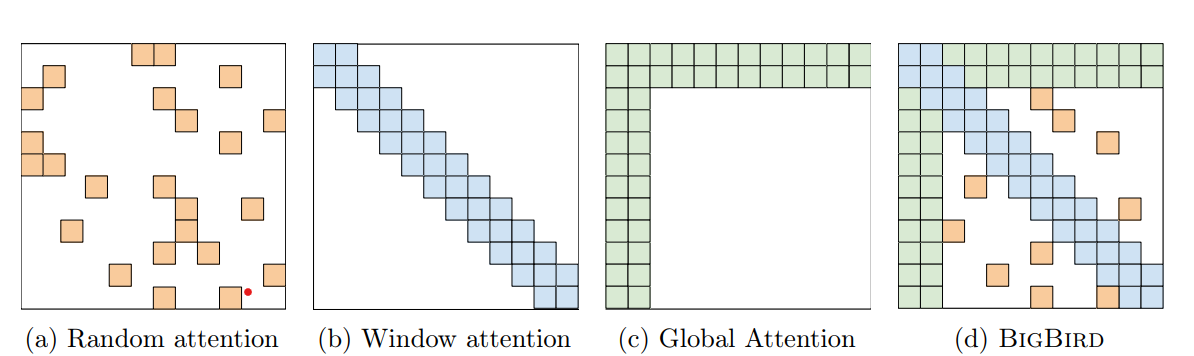
又是一个非常清新脱俗的模型起名~ 大鸟模型和longformer相比增加了随机注意力机制，不过感觉主要的创新是对全局注意力机制进行了改良，提出了固定注意力patten的ETC全局注意力机制。

1. 随机注意力机制

在滑动窗口注意力之外，模型会每行随机采样r个token来进行交互，不过这里的随机注意力并不和以下的ETC全局注意力一同使用~

1. 全局注意力

只使用滑动窗口注意力+随机注意力，作者发现效果和BERT相比还是有所损失，因此加入了全局注意力。和longformer的区别在于，Bigbird除了支持对部分已有token（一般是序列的第一个和最后一个字符）进行全局attention之外，简称Bigbird-ITC。还 支持加入额外token（类似CLS）来做全局注意力，简称Bigbird-ETC，ETC不和随机注意力一同使用。从下游任务效果上来看ETC的效果略好于ITC+随机注意力，效果对比基本是用的BigBird-ETC，不过这也限制了BigBird只能用在NLU场景~

整体效果，在QA和长文本摘要任务上上Bigbird基本是新SOTA

Reformer

• paper: REFORMER: THE EFFICIENT TRANSFORMER

• github: https://github.com/google/trax/tree/master/trax/models/reformer

• Take Away: LSH搜索序列中的高权重token，做固定长度局部注意力计算

先来看下原始Transformer的空间复杂度: \(max(b*l* d_{ffn}, b *n_{h} * l^2)*n_{l}\)。其中b是batch，l是文本长度，\(d_{ffn}\)是Feed Forward层大小，\(n_{h}\)是多头的head size，\(n_l\)是层数。Reformer引入了三个方案来降低Transformer的计算和内存复杂度

• LSH Attention：近似计算，针对l，只计算注意力中高权重的部分

• 可逆网络：时间换空间，针对\(n_l\)，只存储最后一层的参数

• 分块计算：时间换空间，针对\(d_{ffn}\)，对FFN层做分块计算

后两个方案和长文本无关这里我们简单过，重点是LSH Attention部分的创新~

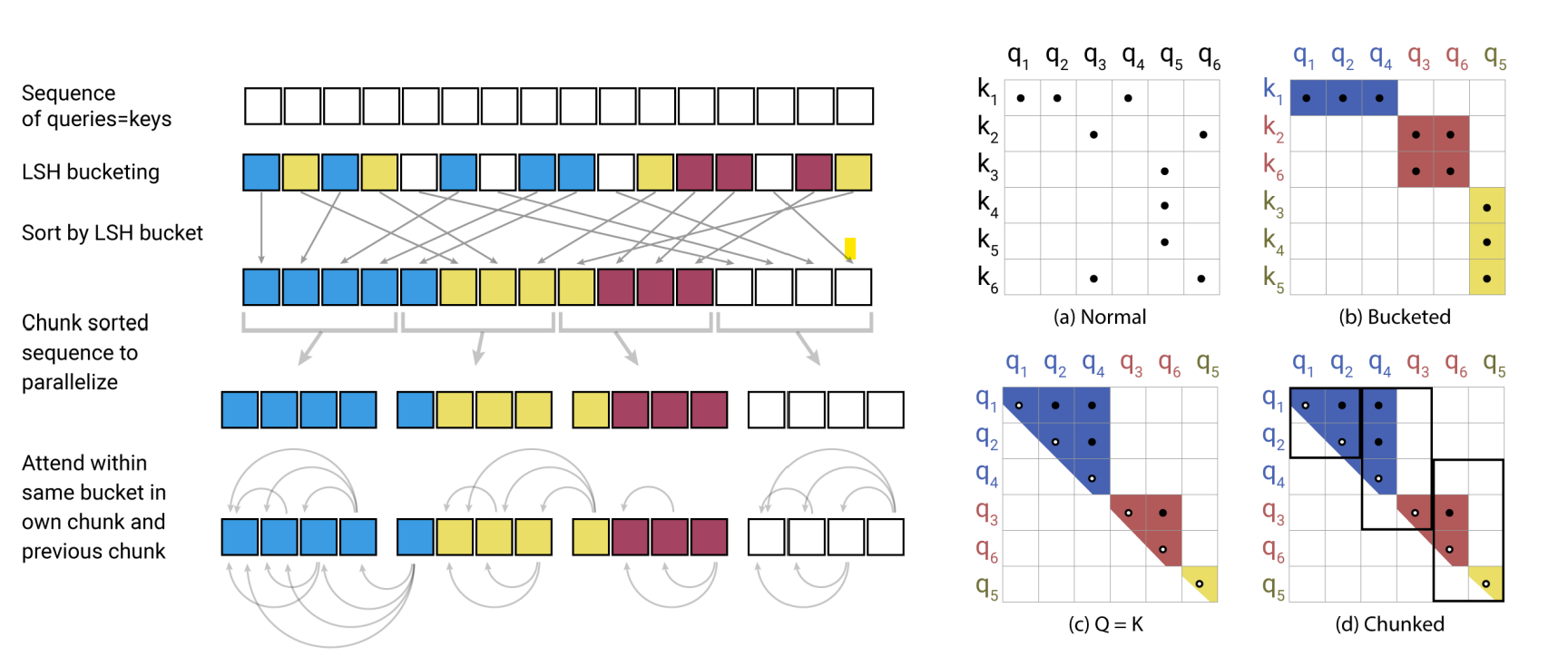
1. LSH Attention

Local Sensitentive Hashing Attention是Reformer的主要贡献，也就是最初分类中的可学习pattern注意力机制。考虑Attention的结果是被高权重的key主导的，因此每个token的注意力权重可以被部分高权重的token近似，只计算局部注意力从而避免计算\(L^2\)的注意力矩阵。难点转换成了如何更高效的找到高权重的key，也就是和query token向量空间更相似的key token来进行局部交互，这里作者使用了LSH，一种在高维数据中快速近似查找的算法。

LSH使用哈希函数对高位空间的向量x计算哈希函数h(x)，\(h(x)\)满足在高维空间中更近的向量有更高的概率落在相同的哈希桶中，反之在高维空间中距离更远的向量有更低的概率会落在相同的哈希桶中。LSH有很多种算法，这里作者使用的是基于角距离的局部敏感哈希算法。随机初始化向量R维度是\(d_{model} * bucket/2\)，哈希结果为旋转（xR）之后最近的一个正或者负的单位向量\(h(x) = argmax([xR;-xR])\)

使用LSH计算Attention会存在几个问题

• query和key的hashing不同：为了解决这个问题作者把计算注意力之前query和key各自的线性映射统一成了一个，\(k_j=\frac{q_j}{||q_j||}\)，这样二者的哈希也会相同，只需要对key进行计算就得到token的哈希分桶。例如上图(b)长度为6的序列被分成3个桶[1,2,4],[3,6],[5]

• 哈希的误差：哈希只是使得相似的向量落入相同桶的概率更高，为了进一步提高这个概率，可以进行多次不同的哈希函数对输出结果取交际，进一步降低近似带来的信息损失。也就是用更多的时间和空间来换取更好的近似效果

• 每个序列哈希分桶的大小可能不尽相同，无法进行batch计算：这里作者又做了一步近似。根据以上的哈希结果对token进行重排序，相同哈希的token放一起，桶内按原始位置排序，按固定长度m进行切分，每个chunk的query对当前chunk和前一个chunk的key计算注意，也就是位于[m,2m]的query对[0,2m]的key计算注意力，这里m和哈希桶数反向相关\(m=\frac{l}{n_{bucket}}\)，也就是和平均哈希桶的大小正相关。实际上LSH只是用来排序，提高固定长度内注意力权重占整个序列的比例，从而通过有限长度的注意力矩阵近似全序列的注意力结果。同样是固定窗口，LSH使得该窗口内的token权重会高于以上Longformer，BigBird这类完全基于位置的固定窗口的注意力机制，不过LSH的搜索和排序也会进一步提高时间复杂度

1. 可逆残差网络

可逆残差的概念是来自The reversible residual network: Backpropagation without storing activations(Gomez2017)。通过引入可逆变换，RevNet使得模型不需要存储中间层的参数计算梯度 ，每一层的参数可以由下一层通过可逆运算得到。属于时间换空间的方案，因为反向传播计算梯度时需要先还原本层的参数，因此时间上会增加50%左右~ 细节我们就不多展开想看math的往苏神这看可逆ResNet：极致的暴力美学, 简单易懂的往大师兄这看可逆残差网络RevNet

1. 分块计算

分块主要针对FFN层。因为Feed Forward一般会设置几倍于Attention层的hidden size，通过先升维再降维的操作提高中间层的信息表达能力，优化信息的空间分布，以及抵消Relu带来的信息损失。但是过大的hidden size会带来极高的空间占用。因为是在embedding维度进行变换每个位置之间的计算独立，因此可以分块进行计算再拼接，用时间来换空间

效果评测部分我们在下面的performer里一起讨论

Performer

• paper: Rethinking Attention with Performers

• github: https://github.com/google-research/google-research/tree/master/performer

• Take Away: 提出核函数使得QK变换后的内积可以近似注意力矩阵，配合乘法结合律把复杂度从平方降低到线性

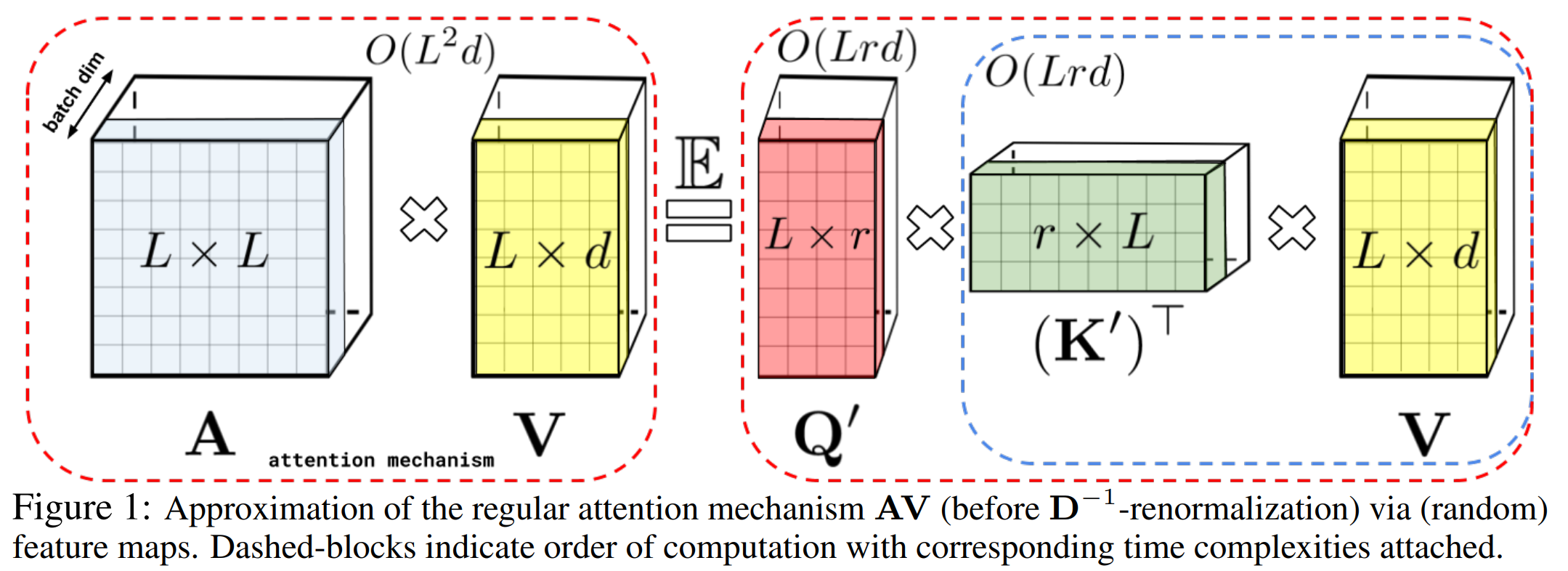
多头注意力机制的计算是query和key先计算Attention矩阵A，再对V进行加权，也就是上图等号左边的计算顺序，复杂度是序列长度的平方。为了避免计算\(L^2\)的注意力矩阵，作者采用矩阵分解\(q^{\prime} \in R^{L,r},k^{\prime} \in R^{L,r}\)，这里r<d<<L，配合矩阵乘法的结合律，K先和V计算再和Q内积，把空间复杂度从平方级降低到线性。但是注意力矩阵过softmax之后无法直接做可逆转换得到\(q^{\prime},k^{\prime}\), 因此作者提出了使用positive Random Feature对QK进行映射，使得映射后的矩阵\(q^{\prime},k^{\prime}\)内积可以近似Attention矩阵。简单解释就是以下的变换

所以Performer的核心在\(\phi\)核函数的设计使得映射后的QK内积可以高度近似注意力矩阵，具体设计如下

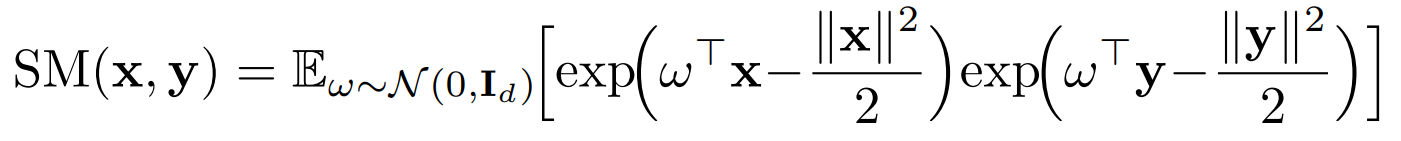
这里\(SM(x,y) = exp(x^Ty)\)也就是原。始的注意力矩阵,按照\(f(x)=exp(w^Tx-\frac{||x||^2}{2})\)对Q和K进行变换后，QK内积的期望就等于原始的注意力矩阵。不过在实际计算中只能对随机变量w进行有限次采样, 因此是近似原始注意力矩阵。论文有大量篇幅在进行推导和证明，这里就不做展开了。

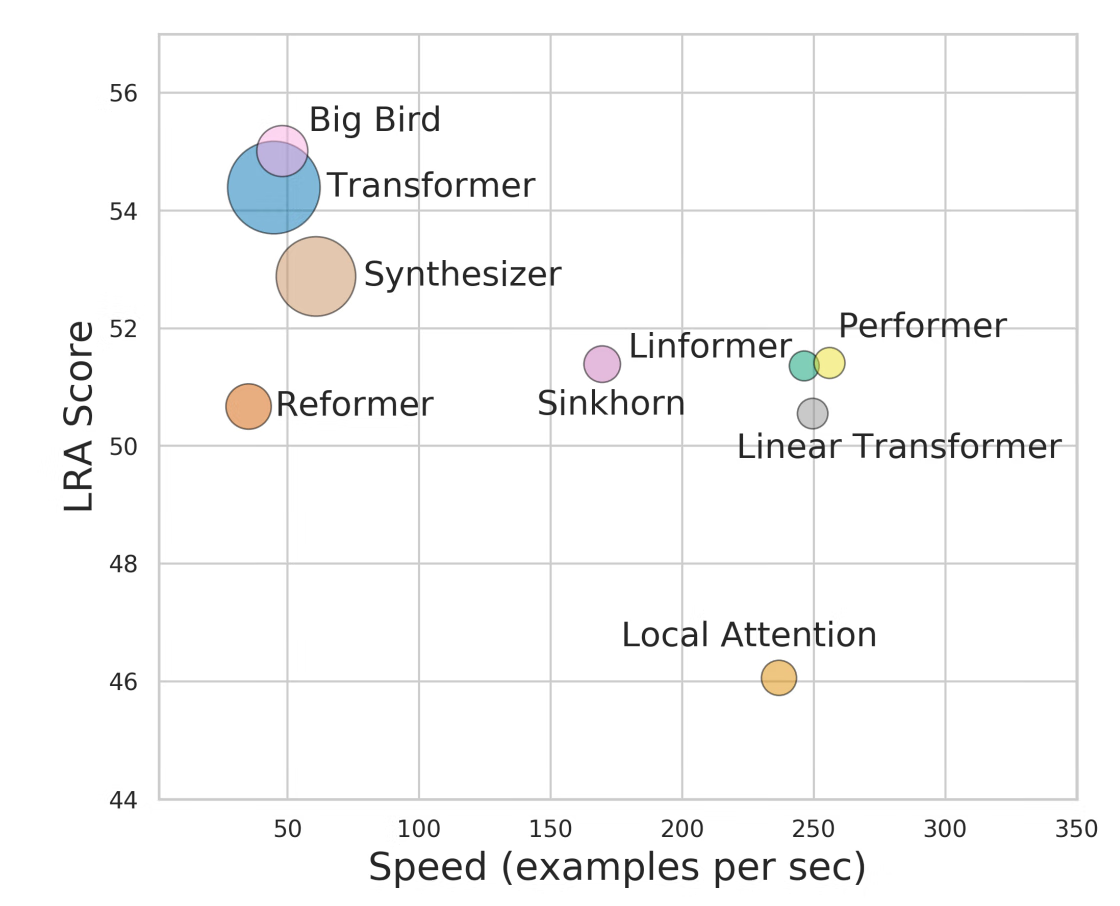
效果对比我们直接参考Google给出的效果对比，横轴是速度，纵轴是效果（多任务平均值），点的大小是内存。整体上BigBird还是拔得头筹，它并不是所有任务的SOTA但是整体效果稳定优秀，想看详细对比结果的参考REF2~

Reference

1. Efficient Transformers: A Survey

2. Long Range Arena: A Benchmark for Efficient Transformers

标签：