掌控(control)
题面描述
公元\(2044\)年,人类进入了宇宙纪元。L国有\(n\)个星球,分别编号为\(1\)到\(n\),每一星球上有一个球长。有些球长十分强大,可以管理或掌控其他星球的球长,具体来说,第\(i\)个星球的球长管理\(k_i+1\)个星球的球长,分别是 \(a_{i1},a_{i2},...,a_{iki}(a_{ij}<i)\),但若想要掌控一个星球的球长,就没那么容易了,第\(i\)个星球的球长掌控第\(j\)个星球的球长当且仅当他管理的所有球长都掌控第\(j\)个星球的球长,当然,所有球长都掌控他自己。 这些球长要召开\(q\)次会议,每次会议由\(t_i\)个球长召开,所有被他们掌控的球长都会参加,你作为宇宙会议室室长,需要知道每次会议有多少个球长参加。
输入
第一行一个数\(n\),表示星球的个数; 接下来\(n\)行,每一行首先给出一个\(k_i\)(可能为\(0\)),接下来\(k_i\)个数,描述第\(i\)个星球的球长管理的球长。保证没有重复; 接下来一行,给出一个数\(q\),表示询问的个数; 接下来\(q\)行,每一行描述一个询问:格式同上文的格式。不保证没有重复(重复的球长当做只出现了一次)
输出
输出共\(q\)行,第\(i\)行输出第\(i\)次询问的答案。
样例输入
7 0 1 1 1 1 1 2 2 2 3 0 2 2 6 3 2 2 3 2 3 5 2 4 5
样例输出
3 3 4
样例解释
对于第一个询问,2、3号球长都掌控1号球长,所以总共有3个球长参会,编号分别为1,2,3; 对于第二个询问,3、5号球长都掌控1号球长,所以总共有3个球长参会,编号分别为1,3,5; 对于第三个询问,4号球长掌控第1、2号球长,所以总共有4个球长参会,编号分别为1,2,4,5; 特别说明:第5号球长没有掌控球长2,因为3属于\(k_5\),但2不属于\(k_3\)。但球长4掌控球长2,因为球长掌控自己。
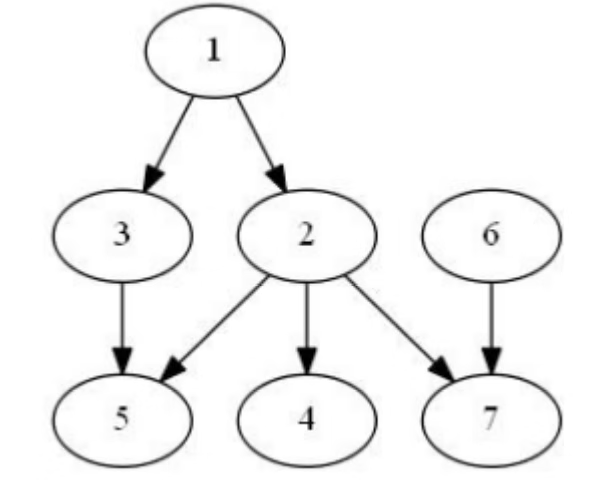
图片说明:u->v表示v管理u
数据范围
题解
暴力做法(40pts)
仔细阅读数据范围,发现部分分的\(n,q\)较小,为了方便处理,我们可以用类似邻接矩阵的思路来存。
考虑所有可能需要储存的信息,我们开以下数组。
bool vis[N];//i是否与会 int con1[N][N];//i管理j int cnt1[N];//i管理的球长数量 int con2[N][N];//i掌控j int cnt2[N];//i掌控的球长数量 int ans1[N][N];//i的第j个管理的球长为n int ans2[N][N];//i的第j个掌控的球长为n
然后依照题意进行模拟,求出每一个球长的掌控情况,最后求出与会者掌控情况的并集即可。
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=2005;
int n,q;
int final;
int meet;//开会
bool vis[N];//i是否与会
int con1[N][N];//i管理j
int cnt1[N];//i管理的球长数量
int con2[N][N];//i掌控j
int cnt2[N];//i掌控的球长数量
int ans1[N][N];//i的第j个管理的球长为n
int ans2[N][N];//i的第j个掌控的球长为n
int main()
{
freopen("control.in","r",stdin);
freopen("control.out","w",stdout);
scanf("%d",&n);
for(int i=1,k;i<=n;i++)
{
scanf("%d",&k);
cnt1[i]=k;
for(int j=1,m;j<=k;j++)
{
scanf("%d",&m);
con1[i][m]=1;
ans1[i][j]=m;
}
}
for(int i=1;i<=n;i++)
{
ans2[i][1]=i;
con2[i][i]=1;
cnt2[i]=1;
}
for(int i=1;i<=n;i++)
{
if(!cnt1[i]) continue;
for(int j=1;j<=n;j++)//i是否掌控j
{
bool flag=0;
for(int l=1;l<=cnt1[i];l++)
{
int nxt=ans1[i][l];//nxt是i管理的第l个球长
if(!con2[nxt][j])
{
flag=1;//nxt无法掌控j
break;
}
}
if(!flag)
{
con2[i][j]=1;
cnt2[i]++;
ans2[i][cnt2[i]]=j;
}
}
}
scanf("%d",&q);
for(int i=1,t;i<=q;i++)
{
final=0;
scanf("%d",&t);
memset(vis,0,sizeof(vis));
meet=0;
for(int j=1;j<=t;j++)
{
scanf("%d",&meet);
for(int l=1;l<=cnt2[meet];l++)
{
vis[ans2[meet][l]]=1;
}
}
for(int j=1;j<=n;j++)
{
if(vis[j]) final++;
}
printf("%d\n",final);
}
return 0;
}正解
暴力为什么会寄?首先是存状态的方式不科学:消耗空间过大,且维护起来相当笨重。其次是维护的效率低下:纯模拟,导致很多不必要的重复运算。
怎么解决呢?首先来看更好的存状态方式。
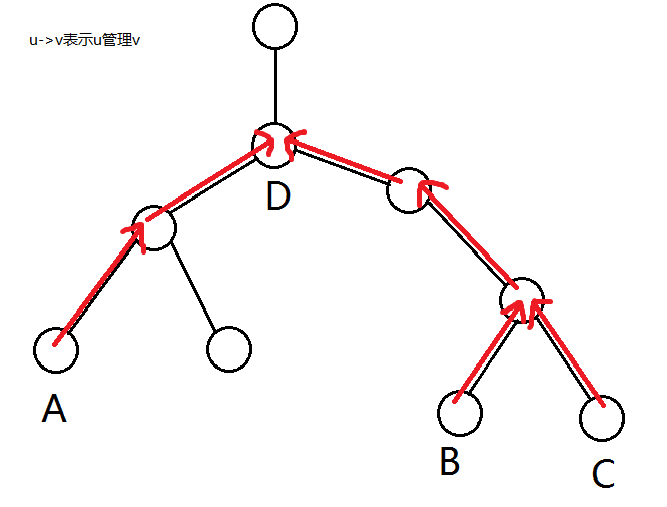
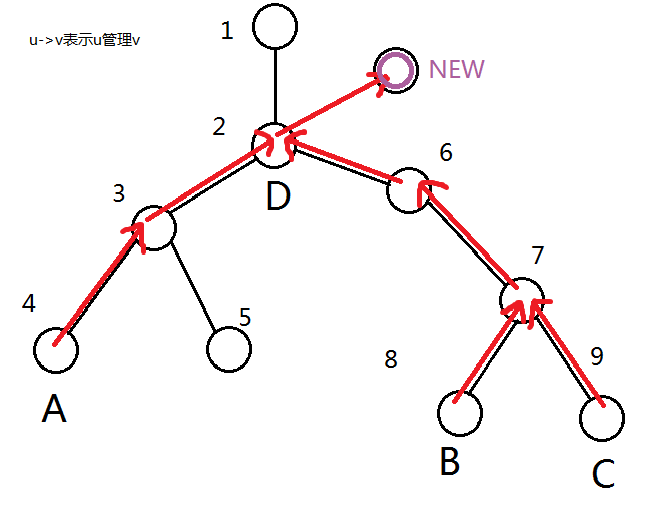
如图,倘若想要掌控\(A,B,C\),那么我们只需要掌控它们的最近公共祖先\(D\)即可,即所有点的掌控关系是一棵树,新进的节点就应该接到它掌控的所有节点的LCA,即上文的\(D\)。而我们自然而然就选择树形结构来存。
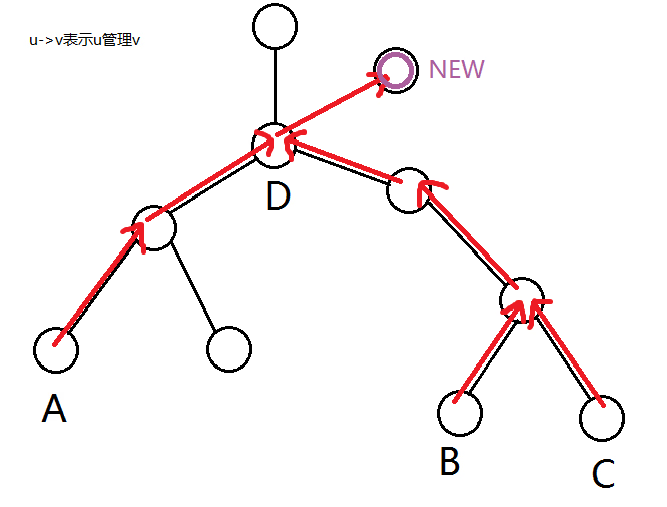
为了提高效率,我们选择边建树边倍增,建树复杂度\(nlogn\)。
void cone(int a,int b)//cone=conect
{
f[a][0]=b;
dep[a]=dep[b]+1;
add(b,a);
for(int i=1;f[f[a][i-1]][i-1];i++)
{
f[a][i]=f[f[a][i-1]][i-1];
}
}
int get_lca(int x,int y)//倍增lca
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}再考虑回答询问。
根据我们建树时遵循的求LCA的原则,发现每个询问就是求给出所有点到根的并集的节点数。考虑将所有节点按\(dfn\)排序,则将每个节点与其相邻的节点的LCA加起来就是答案。
void dfs(int now)//求dfn
{
dfn[now]=++cnt;
for(int i=head[now];i;i=E[i].nex) dfs(E[i].v);
}
for(int i=1,t;i<=q;i++)
{
re(t);
for(int j=1;j<=t;j++) re(meet[j]);
sort(meet+1,meet+t+1,cmp);//按dfn排序
int ans=dep[meet[1]];
for(int j=2;j<=t;j++) ans+=dep[meet[j]]-dep[get_lca(meet[j],meet[j-1])];
printf("%d\n",ans);
}完整AC代码
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
using namespace std;
const int N=200005;
template <typename T>inline void re(T &x) {
x=0;
int f=1;
char c=getchar();
for(;!isdigit(c);c=getchar()) if(c=='-') f=-f;
for(;isdigit(c);c=getchar()) x=(x<<3)+(x<<1)+(c^48);
x*=f;
return;
}
int n,q;
int head[N],totr;
struct edge
{
int u,v,nex;
}E[N<<1];
void add(int u,int v)
{
E[totr++].u=u;
E[totr].v=v;
E[totr].nex=head[u];
head[u]=totr;
}
int f[N][20],dfn[N],meet[N],dep[N];
void cone(int a,int b)//cone=conect
{
f[a][0]=b;
dep[a]=dep[b]+1;
add(b,a);
for(int i=1;f[f[a][i-1]][i-1];i++)
{
f[a][i]=f[f[a][i-1]][i-1];
}
}
int get_lca(int x,int y)//倍增lca
{
if(dep[x]<dep[y]) swap(x,y);
for(int i=19;i>=0;i--)
if(dep[f[x][i]]>=dep[y])
x=f[x][i];
if(x==y) return x;
for(int i=19;i>=0;i--)
if(f[x][i]!=f[y][i])
x=f[x][i],y=f[y][i];
return f[x][0];
}
int cnt;
void dfs(int now)//求dfn
{
dfn[now]=++cnt;
for(int i=head[now];i;i=E[i].nex) dfs(E[i].v);
}
bool cmp(int a,int b)
{
return dfn[a]<dfn[b];
}
int main()
{
freopen("control.in","r",stdin);
freopen("control.out","w",stdout);
re(n);
for(int i=1,k;i<=n;i++)
{
re(k);
int lca=0;
if(k) re(lca);
for(int j=1,mana;j<k;j++)
{
re(mana);
lca=get_lca(lca,mana);
}
cone(i,lca);
}
re(q);
dfs(0);
for(int i=1,t;i<=q;i++)
{
re(t);
for(int j=1;j<=t;j++) re(meet[j]);
sort(meet+1,meet+t+1,cmp);//按dfn排序
int ans=dep[meet[1]];
for(int j=2;j<=t;j++) ans+=dep[meet[j]]-dep[get_lca(meet[j],meet[j-1])];
printf("%d\n",ans);
}
return 0;
}标签:

留言评论