题意

1-n排列，构成一个圆；1-n每个点有个值0或者1，0代表点的度为偶数，1代表点的度为计数；询问能否构成一棵树，树的连边在圆内不会相交，在圆边上可以相交，可以则输出方案。

提示

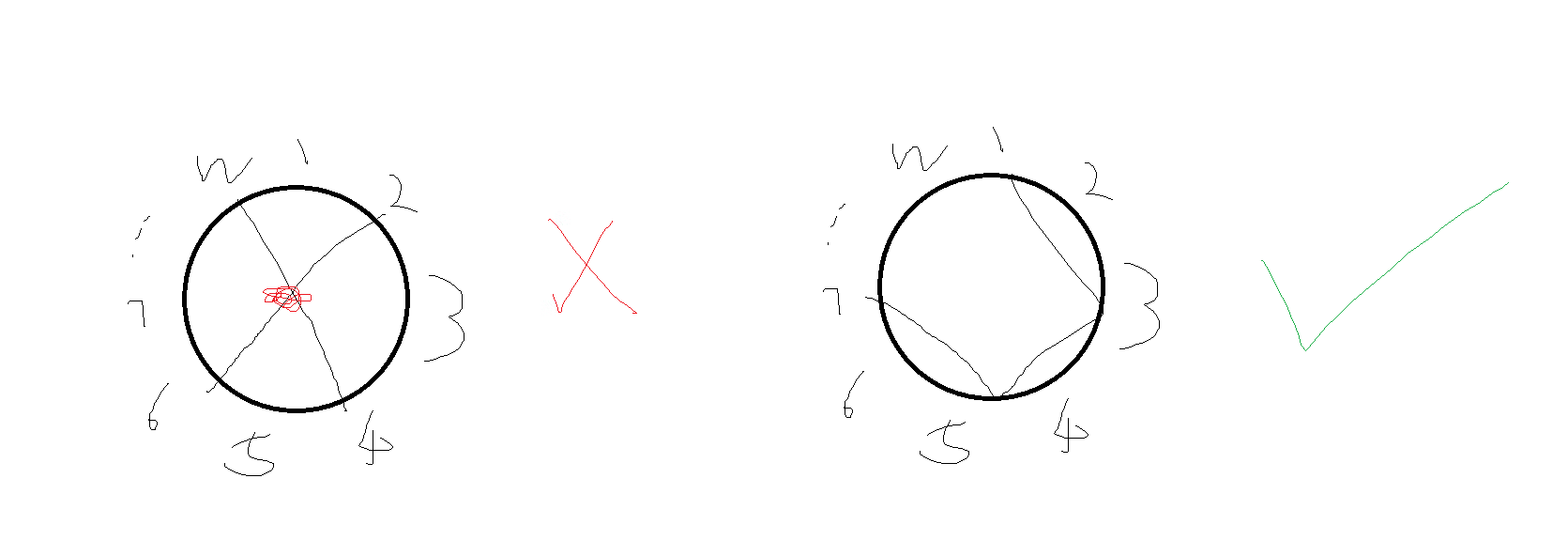
1. 首先考虑什么时候无解，显然，奇数点个数是偶数，并且>=2 2. 由奇数点个数为偶数可以发现，它们可以连到同一个偶数点上（并非直接连） 3. 剩下的偶数点可以直接顺时针串联，直到连到最近的一个奇数点上 4. 相当于每个奇数点后面有一条偶数链，或者没有偶数链只有一个奇点（这都是一样的，因为链最后一个点都只剩下一个需要连的点），直接把链的最后一个点连在一起就好了

代码

#include<bits/stdc++.h>

using namespace std;
char s[200005];

void run() {
    int n;
    cin >> n;
    cin >> s;
    int ans = 0;
    for (int i = 0; s[i] != '\0'; i++) {
        ans += s[i] - '0';
    }
    if (ans % 2 || ans == 0) {
        puts("NO");
        return;
    } else {
        puts("YES");
    }
    int cnt = n - ans;
    if (cnt == 0) {
        for (int i = 2; i <= n; i++) {
            cout << 1 << ' ' << i << '\n';
        }
        return;
    }
    vector<vector<int>> vec;
    for (int i = 1; i <= n; i++) {
        if (s[i - 1] == '1') {
            vector<int> res;
            res.emplace_back(i);
            for (int j = i + 1; j <= n; j++) {
                if (s[j - 1] == '0')res.emplace_back(j);
                else {
                    i = j - 1;
                    break;
                }
            }
            vec.emplace_back(res);
        }
    }
    for (int i = 1; i <= n; i++) {
        if (s[i - 1] == '0') {
            vec.back().emplace_back(i);
        } else
            break;
    }
    int root = 1;
    for (auto k: vec) {

        for (int i = 1; i < k.size(); i++) {
            cout << k[i-1] << ' ' << k[i] << '\n';
        }
    }
    for (int i = 0; i < vec.size(); i++) {
        if (vec[i].size() > 1) {
            root = i;
        }
    }
    for (int i = 0; i < vec.size(); i++) {
        if (i == root)continue;
        cout << vec[root].back() << ' ' << vec[i].back() << '\n';
    }

}

int main() {
    int t;
    cin >> t;
    while (t--)
        run();

    return 0;
}

标签：